查找(Search)
一、查找的第一性原理
查找的本质不是“比较”,而是:
在给定约束条件下,用尽可能低的成本,缩小目标的不确定性空间。
所有查找结构,本质上都在回答三个问题:
- **不确定性如何被缩小?**
- **缩小的代价是什么?**
- **这种代价是否可以被接受?**
因此,查找问题的核心权衡只有四个维度:
- **时间成本**(CPU / IO / 延迟)
- **空间成本**(内存 / 存储冗余)
- **正确性要求**(精确 or 概率)
- **数据约束**(是否有序、是否静态、是否可随机访问)
二、查找问题的整体知识结构
查找(Search)问题体系├── 一、确定性查找(精确定位)│ ├── 顺序查找(无结构)│ ├── 二分查找(有序 + 随机访问)│├── 二、空间换时间的直接映射│ ├── Bitmap│ ├── Hash 映射│├── 三、概率型存在性查找│ ├── 布隆过滤器│ ├── 布谷鸟过滤器│├── 四、时间维度上的查找(调度索引)│ ├── 单层时间轮│ ├── 分层时间轮│└── 五、工程级抽象:索引 ├── 索引的本质 ├── 选型约束与权衡三、确定性查找:用结构消除不确定性
1. 顺序查找(Linear Search)
本质原理
- 无任何先验结构
- 每比较一次,只能排除一个候选项
不确定性收敛速度
- 线性下降
- 时间复杂度:`O(n)`
int seq_search(int array[], int n, int key){ for(int i = 0; i < n; i++) { if(key == array[i]) return i; } return -1;}工程哲学
顺序查找并不“低级”,它是:
- 数据规模很小
- 或查找次数极低时最稳健的选择
2. 二分查找(Binary Search)
本质原理
二分查找不是“技巧”,而是利用全序关系进行信息熵减半。
每一次比较,都会排除 一半的可能性空间。
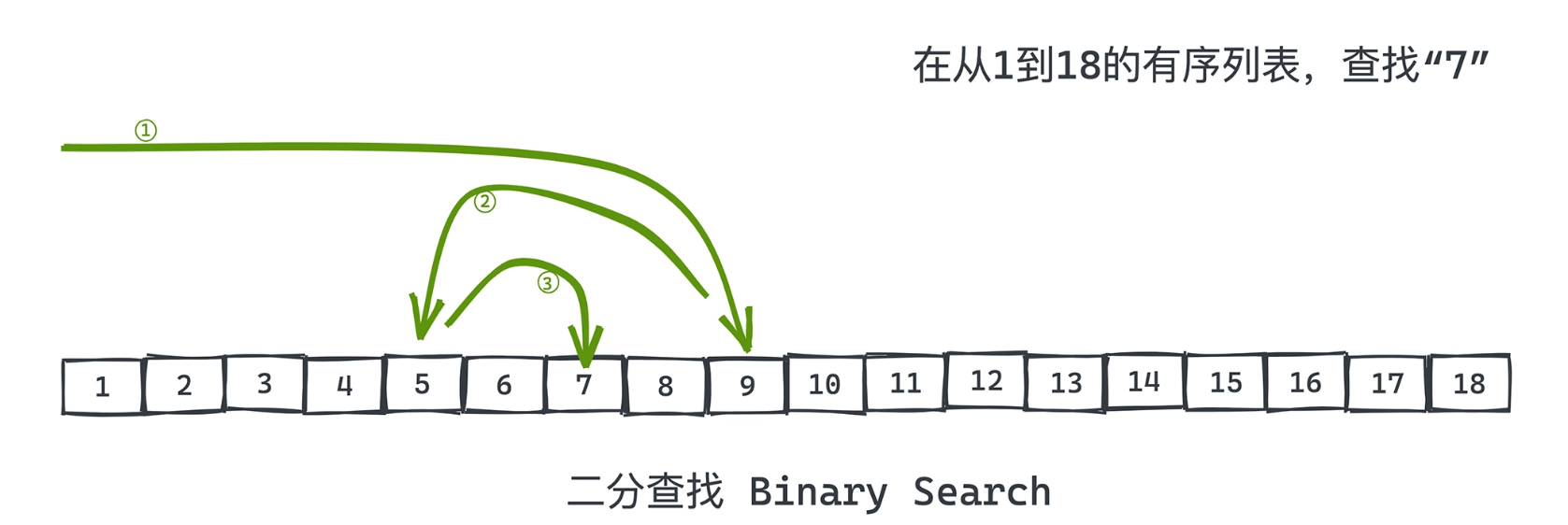
int l = 0, r = a.length - 1;while (l <= r) { int mid = l + (r - l) / 2; if (a[mid].equals(target)) { return mid; } if (less(target, a[mid])) { r = mid - 1; } else { l = mid + 1; }}return -1;隐含约束(本质代价)
- 数据必须有序
- 必须支持随机访问
- 通常依赖连续内存
工程迁移能力
二分查找是一种问题拆解思维:不仅用于数据查找,也用于:
- Bug 定位
- 系统分层排查
- 性能瓶颈收敛
四、空间换时间:用存储消除计算
1. Bitmap(位图)
本质原理
用空间换取 O(1) 的存在性判断。
- 数据值 → 数组下标
- 是否存在 → 位是否为 1
1存在 => 0100002存在 => 0010001,2都存在 => 011000本质代价
空间与值域强相关
适用于:
- ID 连续
- 值域有限
- 强存在性判断
五、概率型查找:允许错误以换取极致效率
1. 布隆过滤器(Bloom Filter)
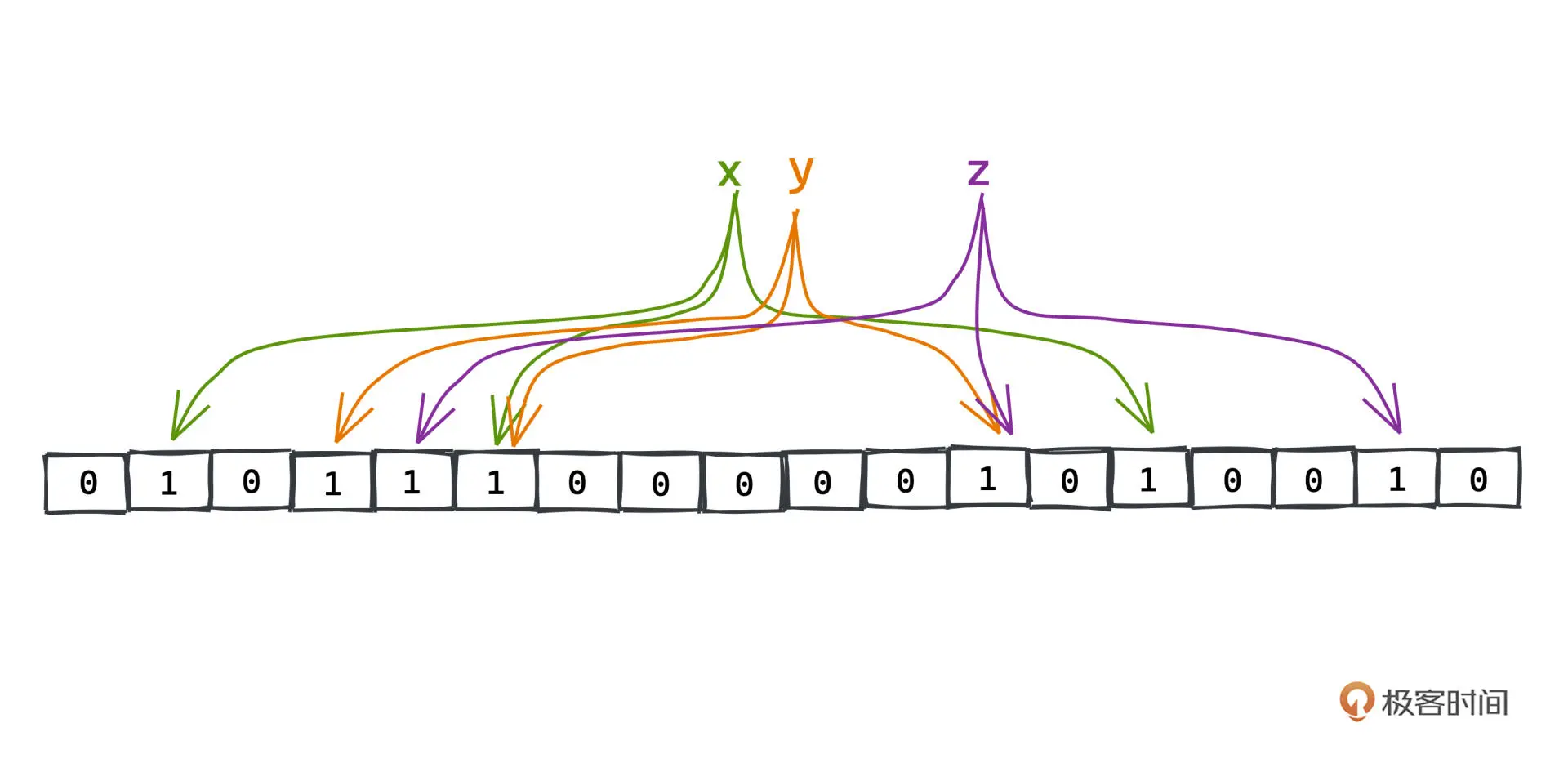
本质原理
用多重哈希 + 位图判断“是否可能存在”。
查询结果只有两种:
- 一定不存在
- 可能存在
关键权衡
不支持精确删除
存在误判(假阳性)
但:
- 查询极快
- 空间极省
工程哲学
布隆过滤器的真正价值在于:提前否定不可能发生的请求。
2. 布谷鸟过滤器(Cuckoo Filter)
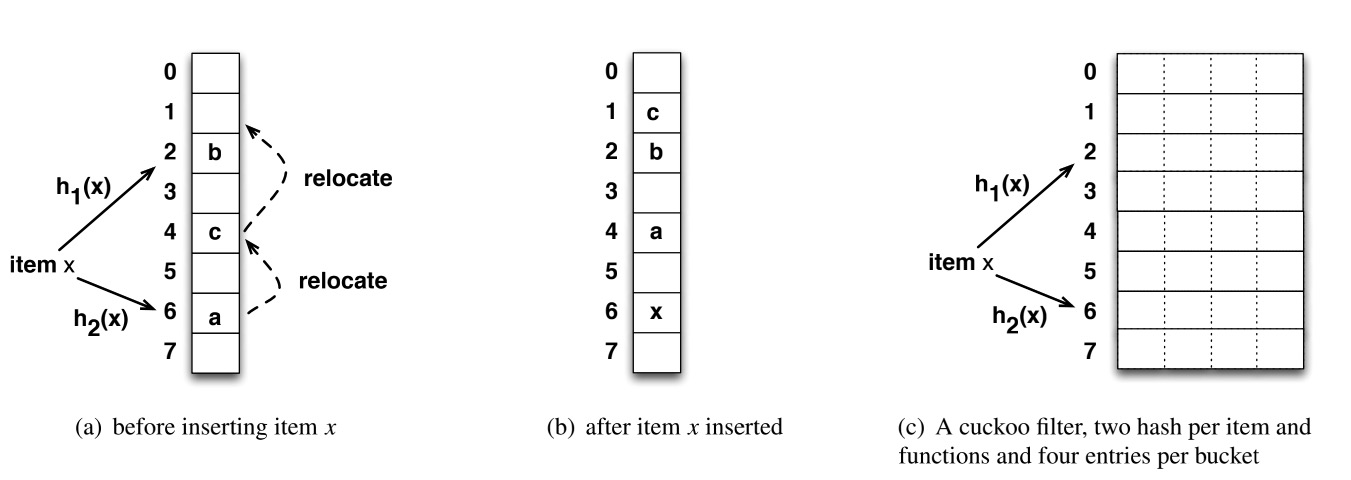
本质原理
- 基于布谷鸟哈希
- 存储的是 key 的 **指纹(fingerprint)**
- 每个 key 有两个候选桶
相比布隆过滤器的演进
支持删除
减少假阳性
引入:
- 误删风险
- 桶溢出复杂度
六、时间维度的查找:时间轮
时间轮本质不是“定时器”,而是在时间轴上建立索引结构。
1. 单层时间轮(Round)
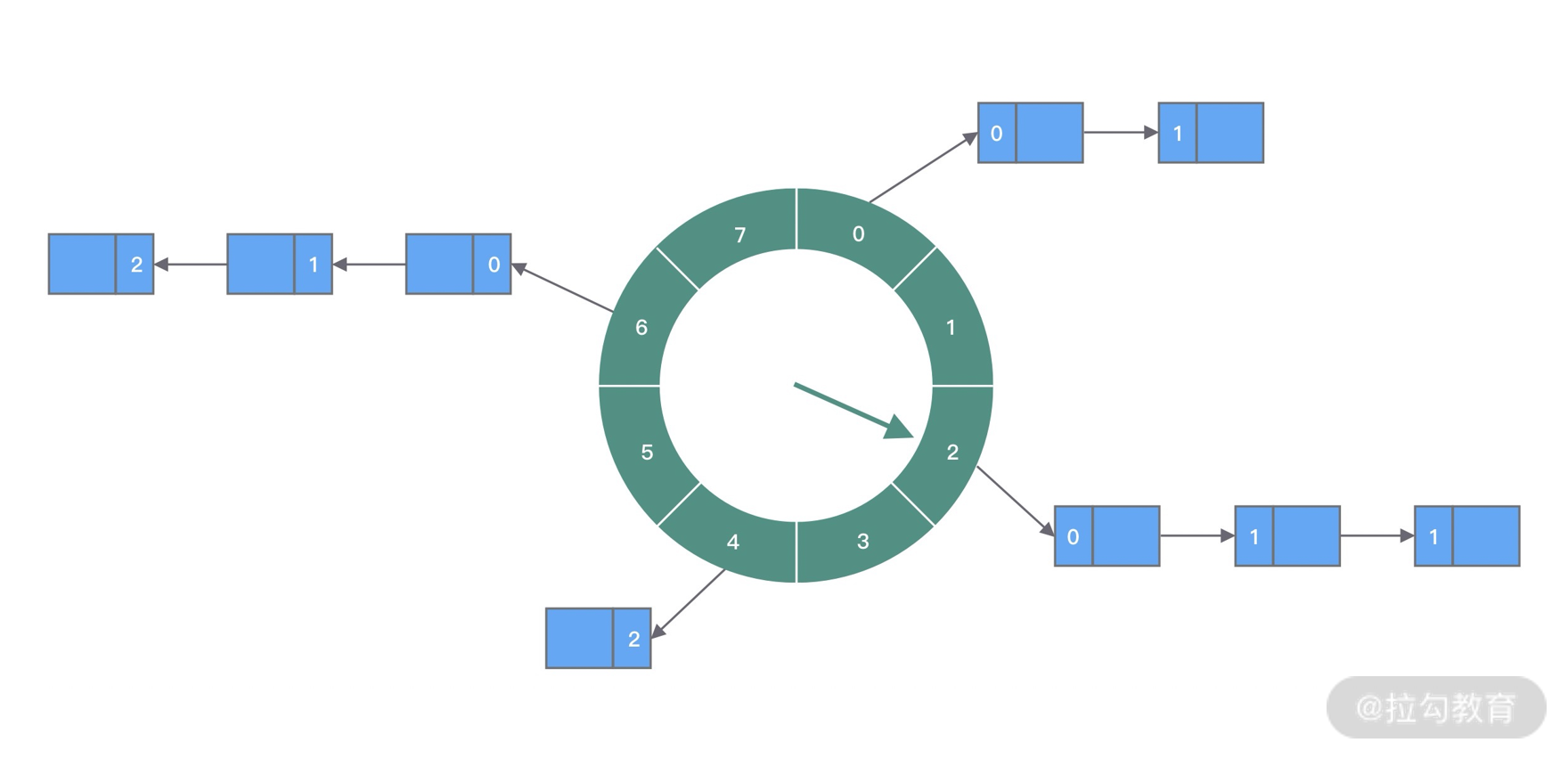
本质思想
- 时间被离散化为 slot
- 当前时间 → 指针位置
- 任务 → 未来 slot
round 的意义
用“圈数”表示未来的距离,将无限时间映射为有限结构。
2. 分层时间轮
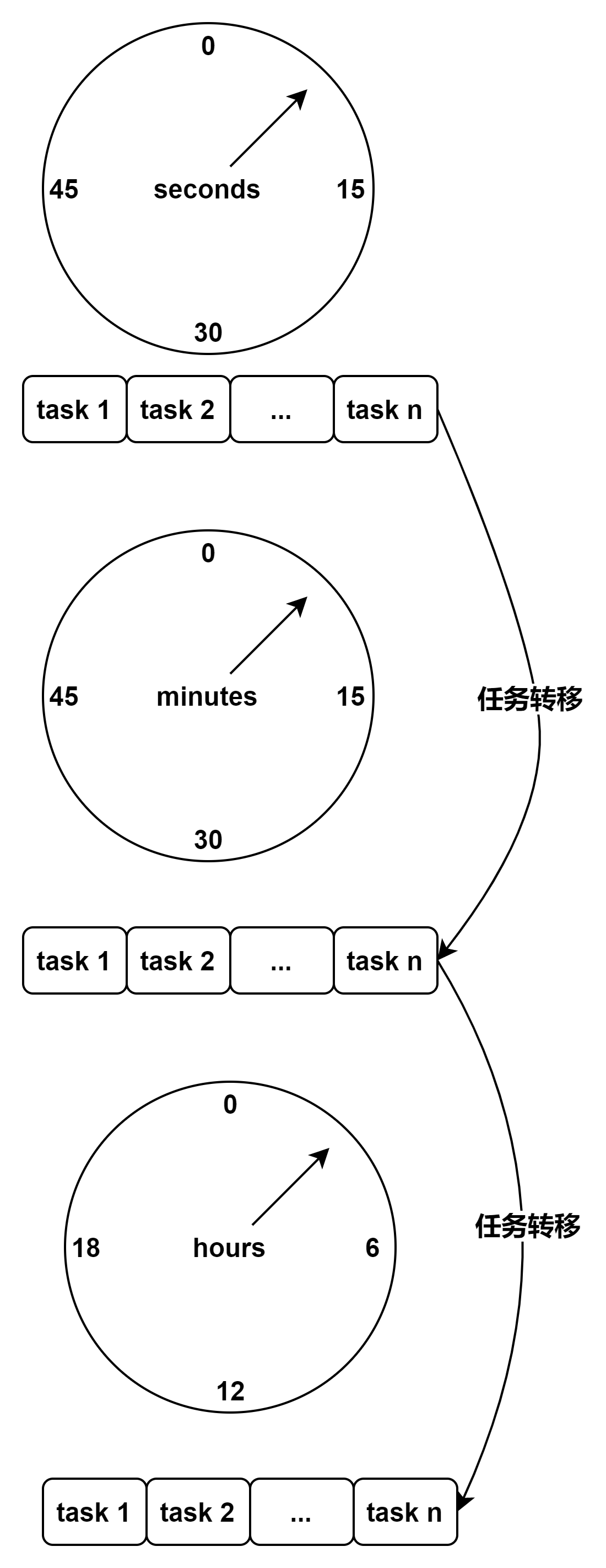
本质演进
单层时间轮无法覆盖大时间跨度
通过 时间分层(小时 → 分钟 → 秒):
- 降低单层轮盘规模
- 保持调度精度
本质类比
分层时间轮 ≈时间维度上的 B+ 树
七、工程级抽象:索引(Index)
1. 索引的本质
索引不是数据结构,而是 “查找约束下的组织方式”。
2. 功能性约束
- 数据形态:结构化 / 非结构化
- 数据变化:静态 / 动态
- 查询类型:单值 / 区间 / 组合
- 存储介质:内存 / 磁盘
3. 非功能性约束
- 空间消耗
- 维护成本
- 更新代价
- 并发与一致性
4. 常见索引结构(按思想分类)
| 思想 | 结构 |
|---|---|
| 映射 | Hash |
| 有序 | 红黑树 / B+ 树 |
| 跳跃 | 跳表 |
| 否定 | 布隆过滤器 |
八、查找结构的演进总览
线性扫描→ 有序结构(二分 / 树)→ 映射定位(Hash / Bitmap)→ 概率容错(Bloom / Cuckoo)→ 维度扩展(时间轮)→ 系统级索引九、总结:查找不是算法,而是认知方式
所有查找结构,都是对"不确定性"的不同妥协方式。
- 二分查找:牺牲顺序自由,换取对数时间
- Bitmap:牺牲空间,换取常数时间
- 布隆过滤器:牺牲准确性,换取吞吐
- 时间轮:牺牲精度,换取规模
关联内容(自动生成)
- [/算法与数据结构/散列表.html](/算法与数据结构/散列表.html) 哈希查找与散列表是实现O(1)查找的重要数据结构,与查找算法中的哈希映射部分密切相关
- [/算法与数据结构/排序.html](/算法与数据结构/排序.html) 排序与查找密切相关,有序数据是二分查找等高效算法的前提条件
- [/中间件/数据库/索引.html](/中间件/数据库/索引.html) 数据库索引是查找算法在工程实践中的重要应用,包括B+树、哈希索引等
- [/数据技术/检索技术.html](/数据技术/检索技术.html) 检索技术是查找算法在大数据领域的扩展应用,包括倒排索引、哈希检索等
- [/中间件/数据库/ElasticSearch.html](/中间件/数据库/ElasticSearch.html) 搜索引擎中的查找技术,体现了查找算法在分布式系统中的实际应用
- [/中间件/数据库/redis/数据结构.html](/中间件/数据库/redis/数据结构.html) Redis中的数据结构和查找实现,特别是Hash数据结构的查找优化
- [/算法与数据结构/树.html](/算法与数据结构/树.html) 二叉查找树等树形结构是实现高效查找的重要数据结构
- [/中间件/数据库/数据库优化.html](/中间件/数据库/数据库优化.html) 数据库优化与查找算法密切相关,特别是索引优化和查询优化
- [/计算机网络/http/爬虫/爬虫.html](/计算机网络/http/爬虫/爬虫.html) 爬虫系统中的URL去重等技术使用了布隆过滤器等查找算法