排序算法

一、排序的第一性原理

1. 排序的本质

排序 = 将一个无序集合，转换为满足某种全序关系的序列。

从信息视角看，排序解决的是：

2. 有序度与逆序度模型

$$\text{有序度} = \sum_{i

排序过程的本质：不断减少逆序对的过程。

不同排序算法的区别，不在于“是否排序”，而在于：

3. 排序算法的两种信息来源

类型核心思想代价与约束
比较排序通过比较逐步获取信息下界 O(nlogn)
非比较排序利用数值分布直接映射对数据分布有前提

二、排序算法的认知结构树

排序算法├── 比较排序│   ├── 插入型（插入、希尔）│   ├── 交换型（冒泡、快速）│   ├── 选择型（选择、堆）│   └── 分治型（归并、快速）└── 非比较排序    ├── 计数（计数排序）    ├── 映射（桶排序）    └── 位分解（基数排序）

分类的目的不是记忆，而是理解算法之间的血缘关系。

三、排序算法的评价维度（设计代价）

维度本质含义
时间复杂度消除逆序所需的操作数量
空间复杂度是否用空间换信息
稳定性是否破坏等值元素的相对顺序
原地性是否允许额外存储结构

稳定性本质：

稳定排序 = 不跨越相等元素

四、基础比较排序（O(n²) 的意义）

O(n²) 排序不是“低级算法”，而是：

1. 选择排序（选择型）

202002070942

核心思想：

哲学代价：

2. 插入排序（插入型）

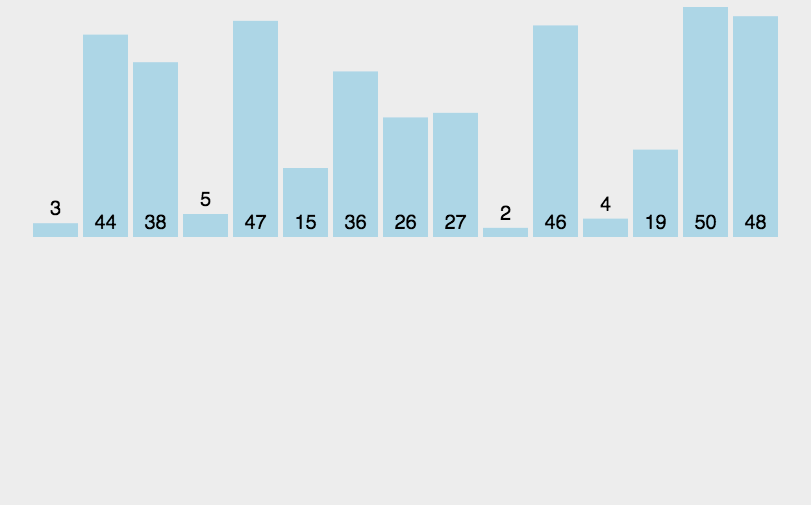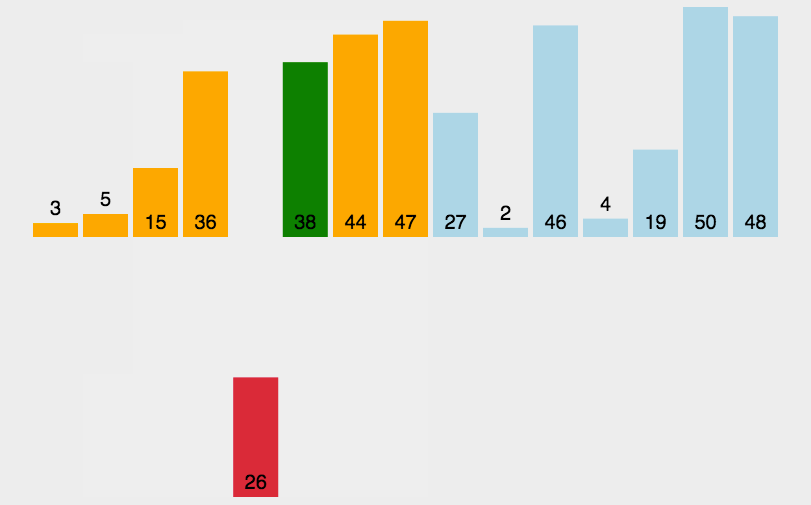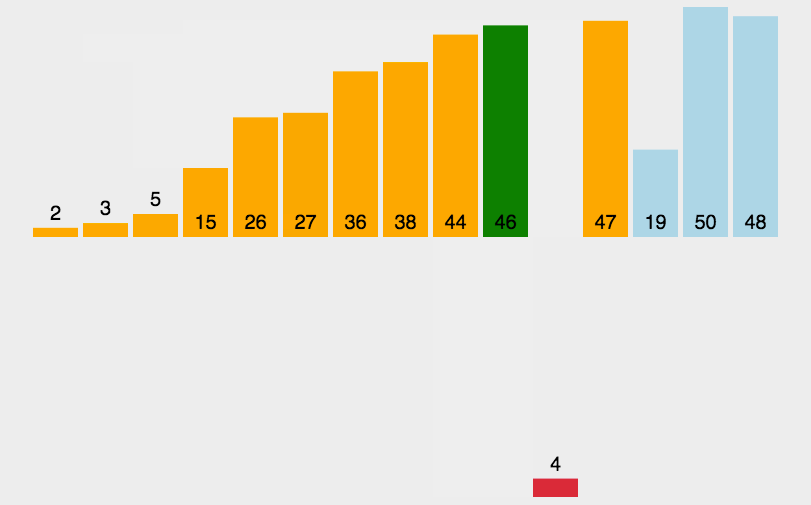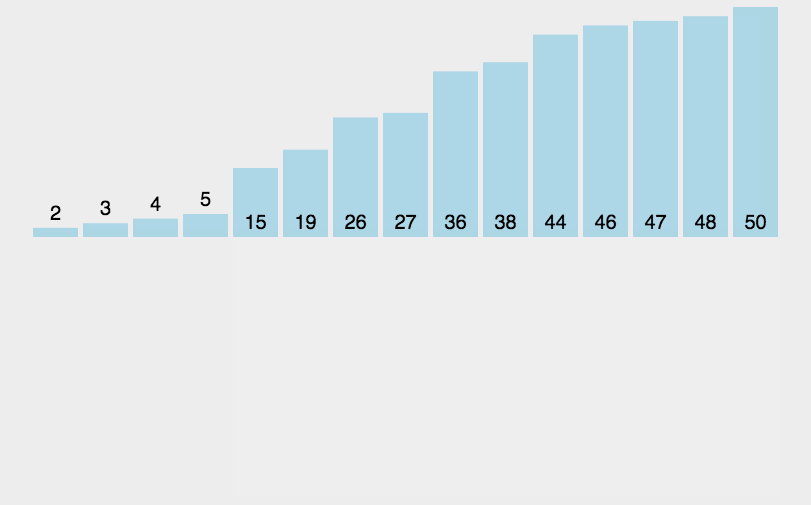
202002070926

核心思想：

本质优势：

3. 冒泡排序（交换型）

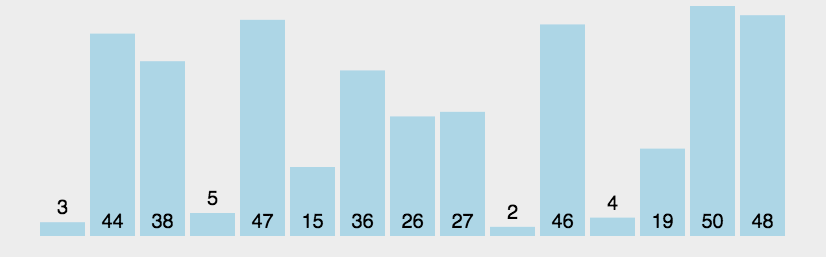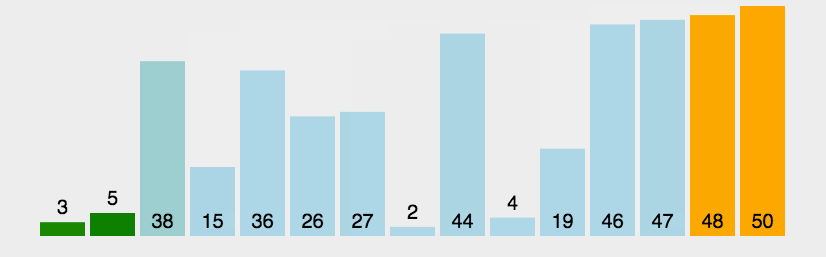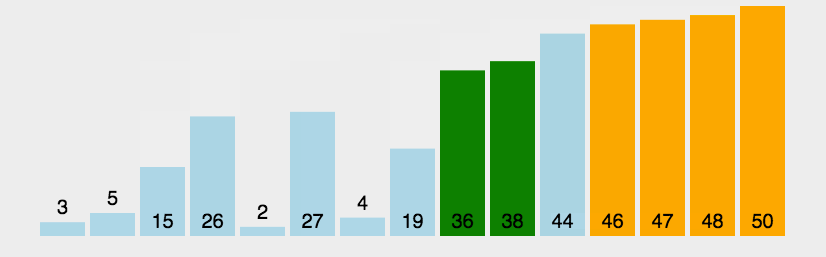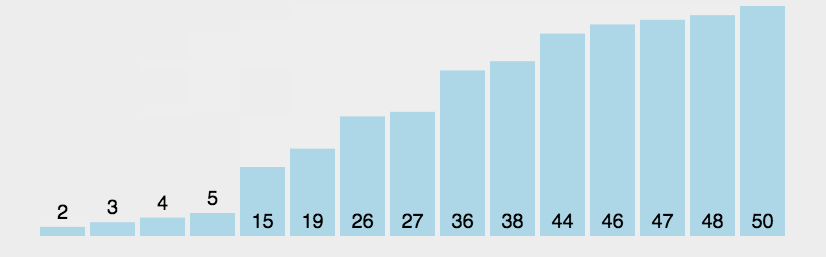
202002081000

核心思想：

本质问题：

五、插入思想的跃迁：希尔排序

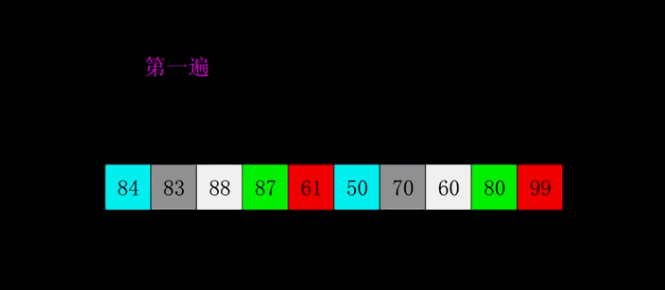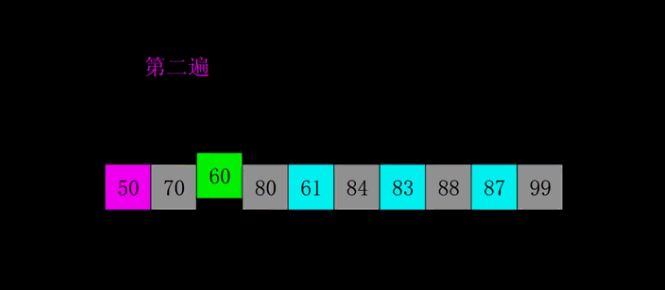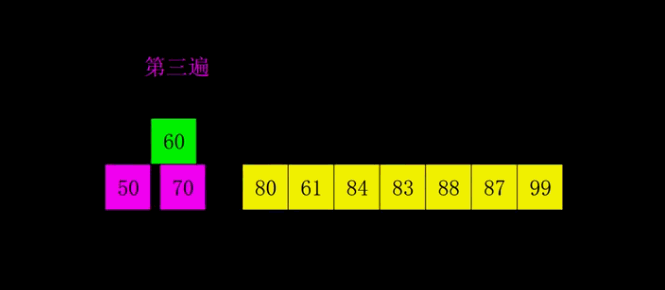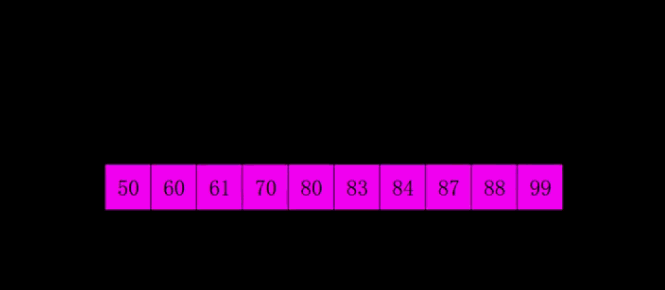
202002081040

本质创新：

用“间隔插入”提前消除远距离逆序。

代价：

六、分治范式的两种极端

1. 归并排序（稳定 + 空间换时间）

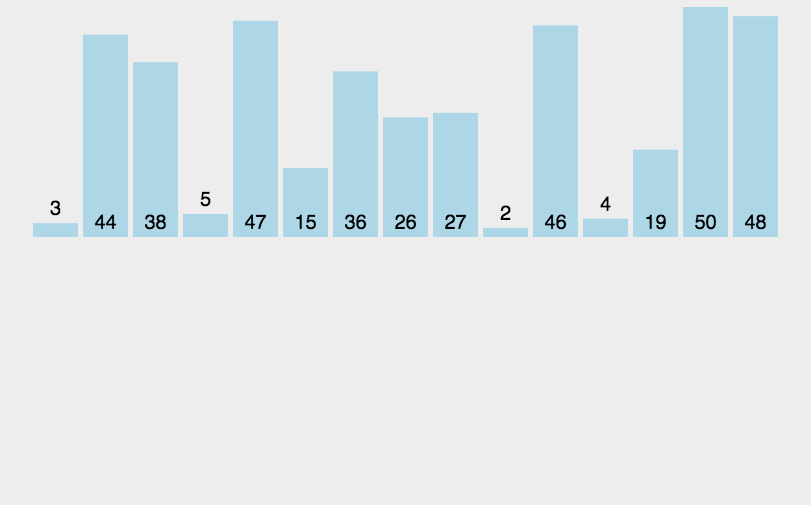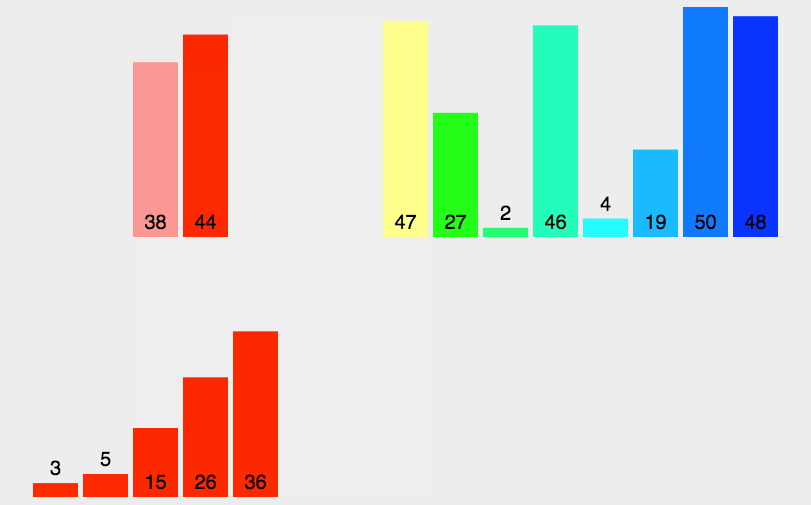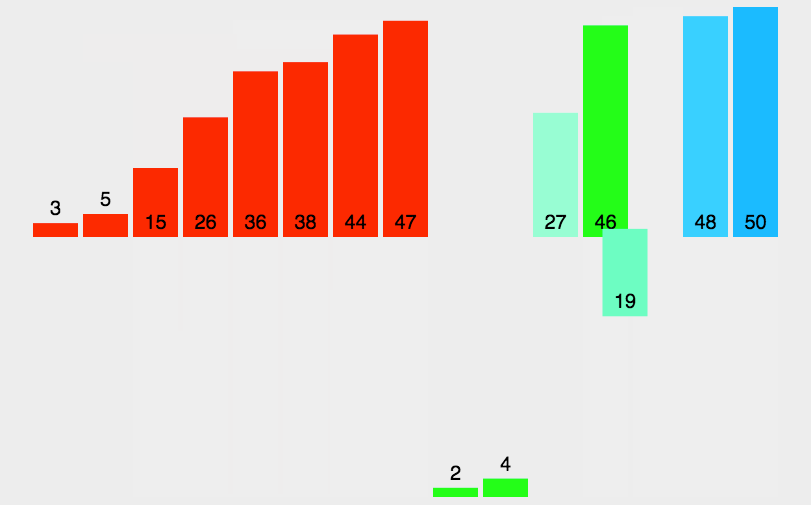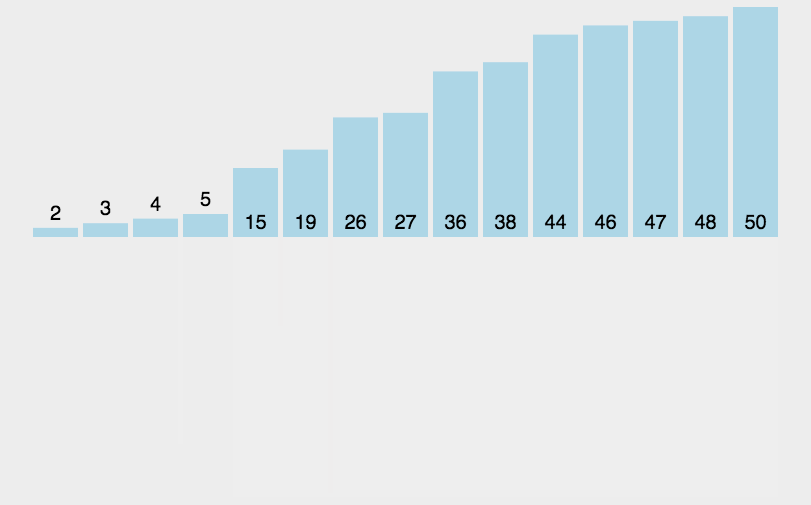
202002081126

本质模型：

哲学取舍：

外部归并排序

202279133543

面向磁盘与 IO 的排序范式。

2. 快速排序（局部性最优解）

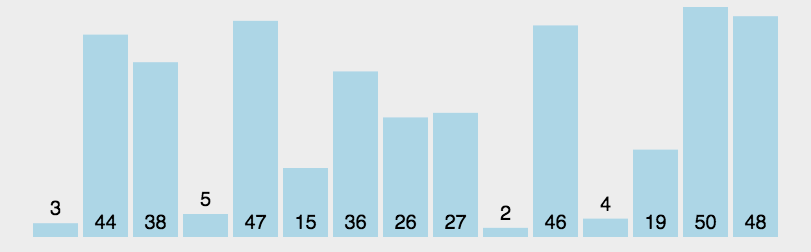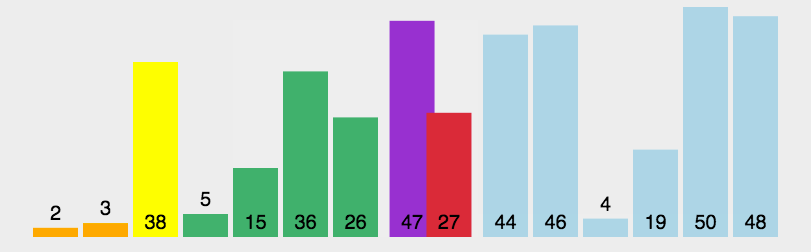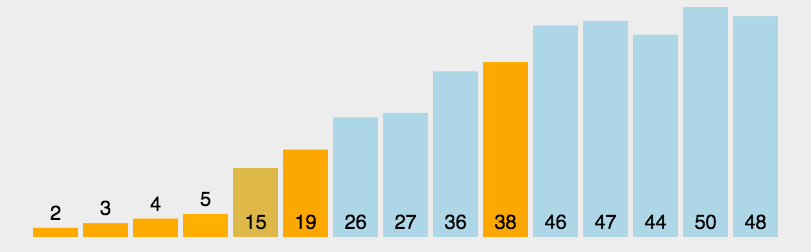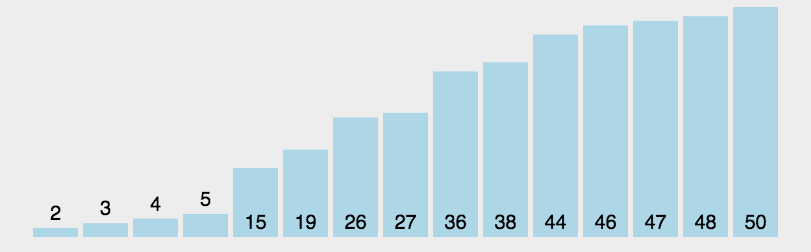
202002081411

本质模型：

风险：

双路 / 三路快排

本质是：控制等值元素导致的结构退化。

七、突破比较下界：线性排序

1. 桶排序（分布假设）

stateDiagram-v21 2 3 4 5 6 7 8 91 --> [1,3]2 --> [1,3]3 --> [1,3]4 --> [4,6]5 --> [4,6]6 --> [4,6]7 --> [7,9]8 --> [7,9]9 --> [7,9]

本质前提：

2. 计数排序（值到位置的映射）

核心思想：

约束：

3. 基数排序（位分解）

hke          iba        hac         haciba          hac        iba         hkehzg  ->      hke  ->    hke    ->   hzgikf          ikf        ikf         ibahac          hzg        hzg         ikf

本质模型：

将复杂比较，分解为多轮稳定的简单排序。

八、特殊排序的认知定位

猴子排序 / 睡眠排序

不是工程算法，而是：

九、洗牌算法（排序的对偶问题）

Fisher-Yates / Knuth-Durstenfeld

排序：消除不确定性洗牌：制造不确定性

二者在概率模型上是对偶问题。

十、工程选型决策模型

场景推荐算法原因
小规模插入排序常数低
近乎有序插入 / 希尔逆序少
稳定要求归并 / 计数顺序保持
内存受限堆排序原地
海量数据外部归并IO 友好

结语

排序算法不是技巧集合，而是工程世界中"秩序建立"的思想样本。

理解排序，本质是在理解：

关联内容（自动生成）