检索技术
合理地组织数据的存储可以提高检索效率。检索的核心思路,其实就是通过合理组织数据,尽可能地快速减少查询范围
线性结构检索
链表与数组就是线性结构检索的代表
非线性结构检索
树与跳表是这种结构的代表
哈希检索
状态检索
- 位图
- 布隆过滤器
倒排索引
全文检索的过程:
| DocId | Doc |
|---|---|
| 1 | 谷歌地图之父跳槽 Facebook |
| 2 | 谷歌地图之父加盟 Facebook |
| 3 | 谷歌地图创始人拉斯离开谷歌加盟 Facebook |
| 4 | 谷歌地图之父跳槽 Facebook 与 Wave 项目取消有关 |
| 5 | 谷歌地图之父拉斯加盟社交网站 Facebook |
对这些doc进行分词之后,以词为主键,记录哪些doc出现了这些词
| WordId | Word | DocIds |
|---|---|---|
| 1 | 谷歌 | 1,2,3,4,5 |
| 2 | 地图 | 1,2,3,4,5 |
| 3 | 之父 | 1,2,4,5 |
| 4 | 跳槽 | 1,4 |
| 5 | 1,2,3,4,5 | |
| 6 | 加盟 | 2,3,5 |
| 7 | 创始人 | 3 |
| 8 | 拉斯 | 3,5 |
| 9 | 离开 | 3 |
| 10 | 与 | 4 |
| .. | .. | .. |
倒排索引包含两个部分:
- 单词词典(Term Dictionary) 记录所有文档的单词,记录单词到倒排列表的关联关系。单词词典一般比较大,可以通过B+树或哈希拉链法实现,以满足高性能的插入与查询
- 倒排列表(Posting List) 记录了单词对应的文档结合,由倒排索引项组成
- 倒排索引项(Posting):
- 文档 ID
- 词频TF:该单词在文档中出现的次数,用于相关性评分
- 位置(Position):单词在文档中分词的位置。用于语句搜索(phrase query)
- 偏移(Offset):记录单词的开始结束位置,实现高亮显示
跳表法加速倒排索引:使用跳表存储文档列表,主要对搜索结果集合运算时进行加速
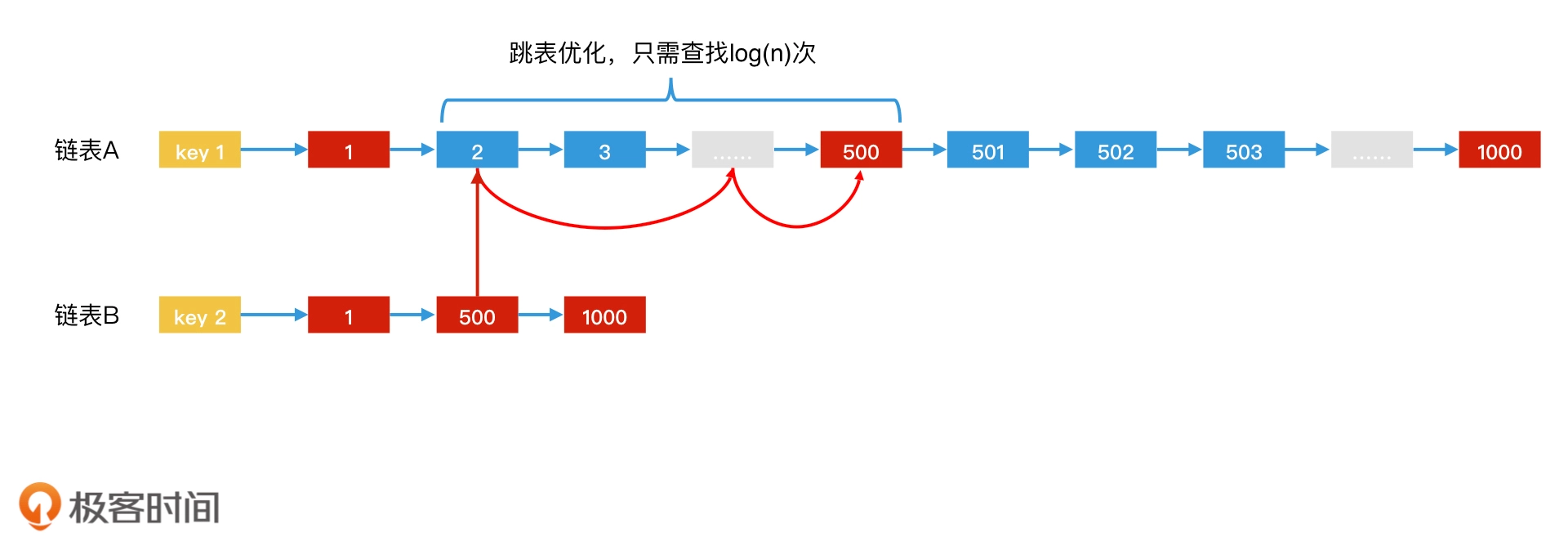
哈希表法加速倒排索引:当两个集合要求交集时,如果一个集合特别大,另一个集合相对比较小,那我们就可以用哈希表来存储大集合。这样,我们就可以拿着小集合中的每一个元素去哈希表中对比
位图法加速倒排索引:
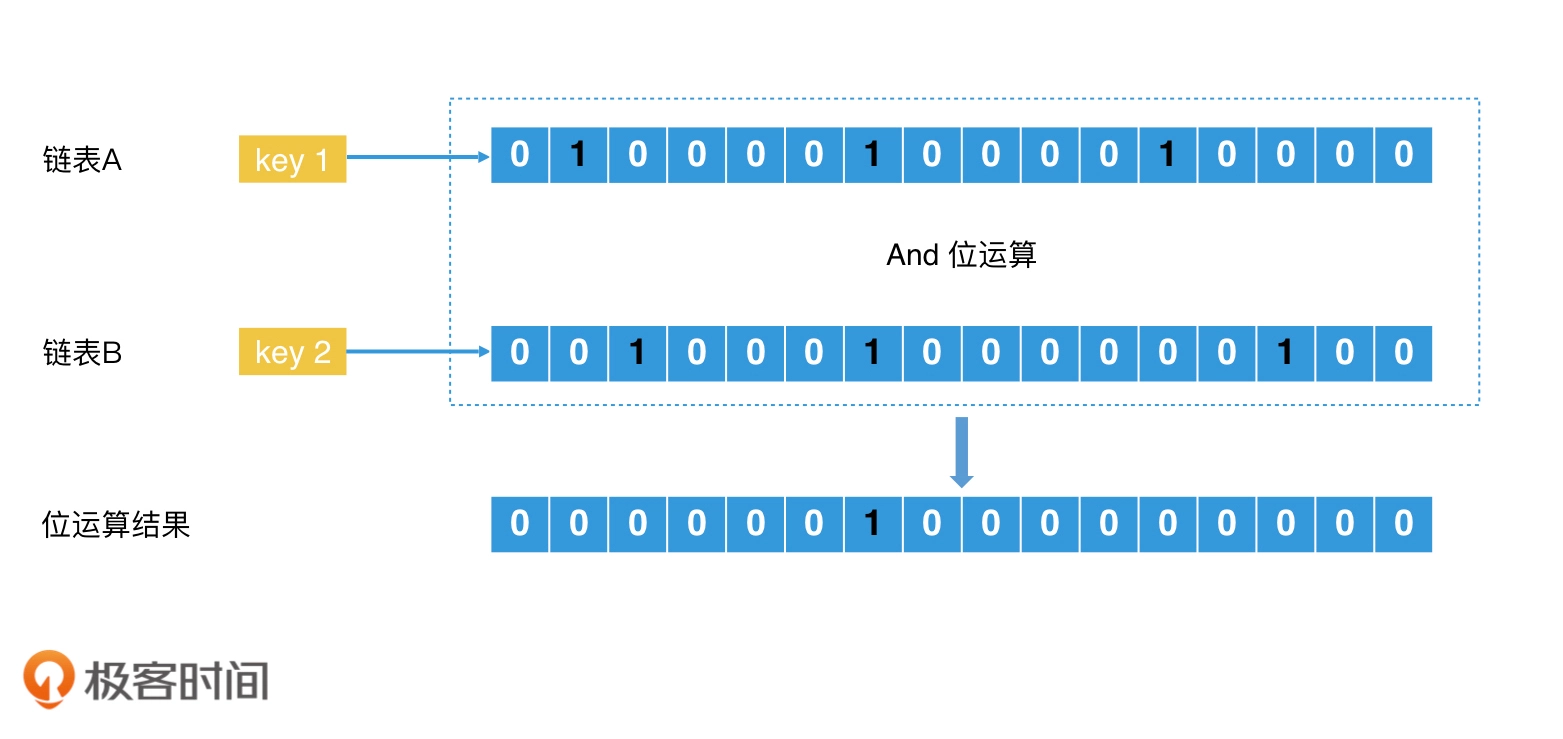
升级版位图:Roaring Bitmap:为了解决传统位图的空间消耗问题:
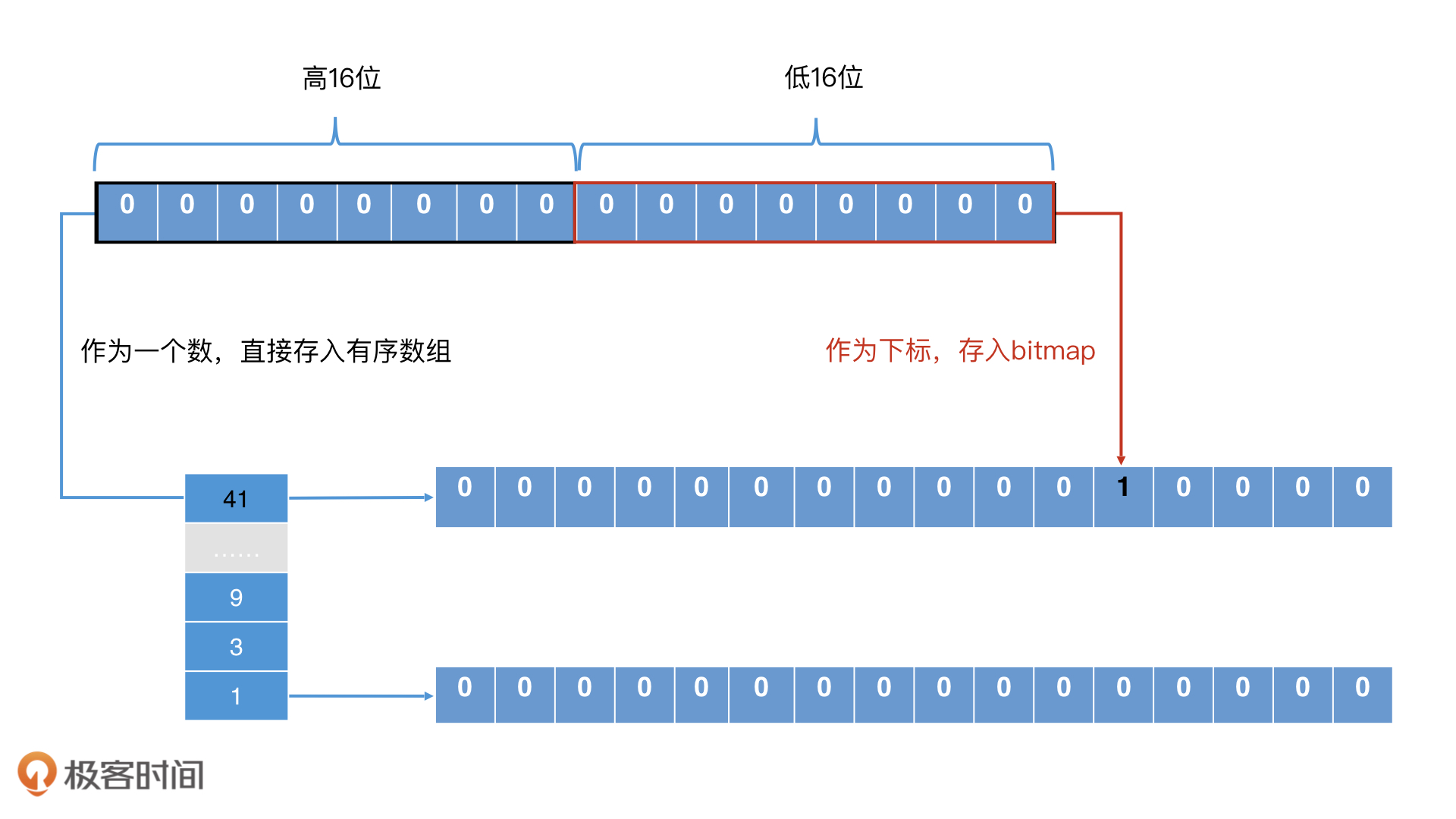
要确认一个元素是否在 Roaring Bitmap 中存在,通过两次查找就能确认了。第一步是以高 16 位在有序数组中二分查找,看对应的桶是否存在。如果存在,第二步就是将桶中的位图取出,拿着低 16 位在位图中查找,判断相应位置是否为 1
对联合查询加速:
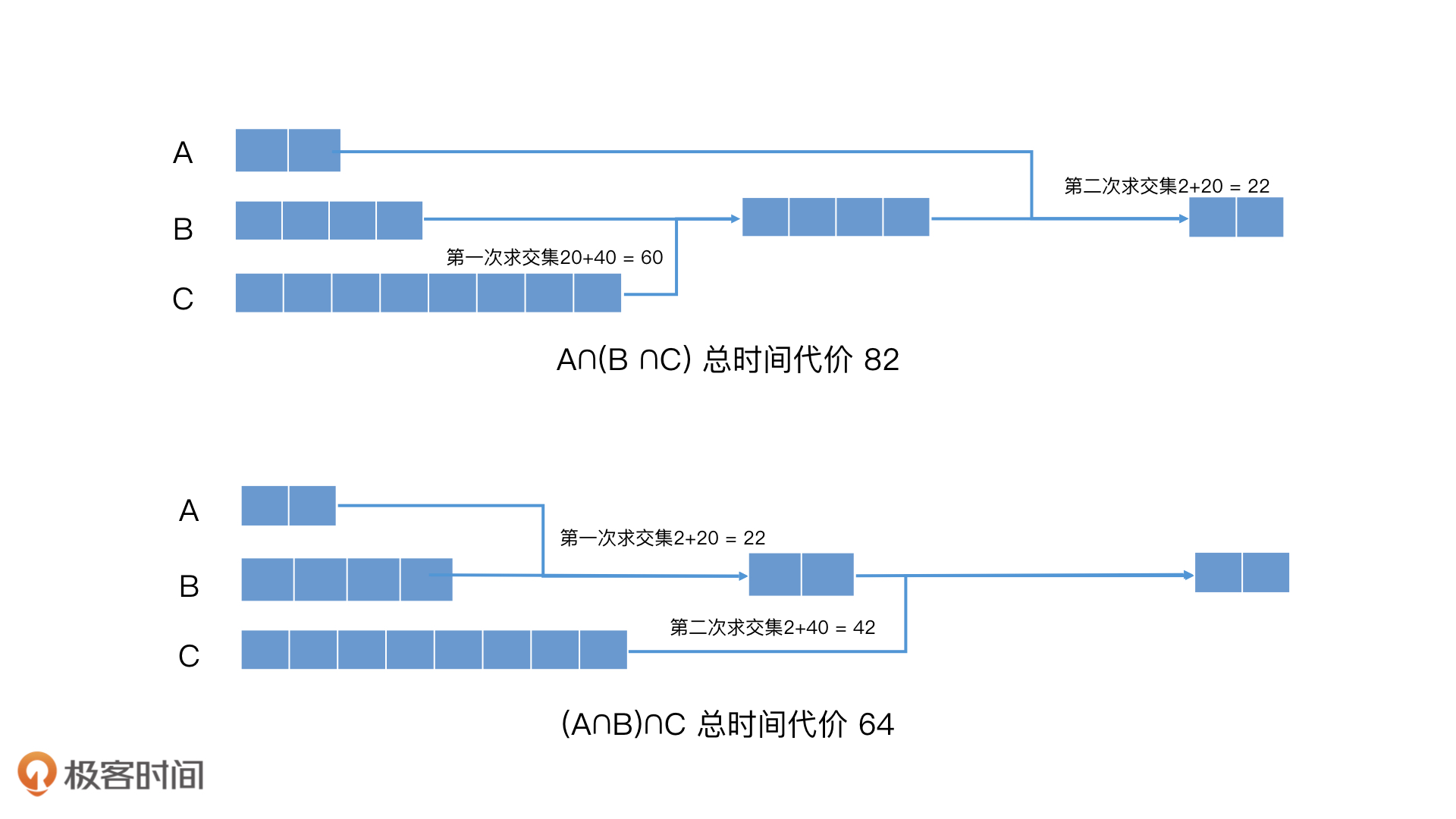
- 使用多路归并,利用跳表的性质,快速跳过多个元素,加快多路归并的效率
- 预先组合法:提前计算好某些查询的结果,需要时直接返回
- 缓存
中间件
目前开源可用的全文检索中间件只有ElasticSearch与Solr 二者都是基于Lucene
ES在许多方面都超过了Solr 所以目前只能选择ES
数据库检索
索引和数据分离:能将索引的数组大小保持在一个较小的范围内,让它能加载在内存中,这样就能减少对磁盘的访问
- [B+树](/中间件/数据库/索引.html#B+ Tree原理)
NoSQL检索
- [LSM树](/中间件/数据库/索引.html#LSM树)
大规模索引构建
索引创建
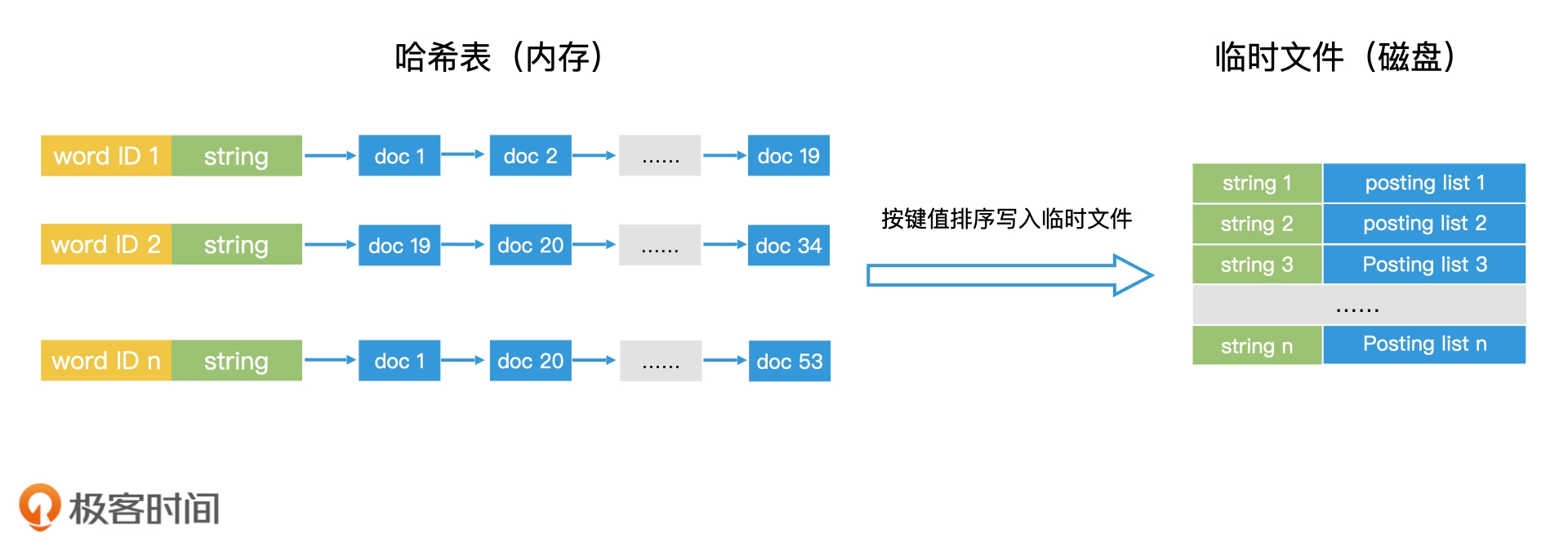
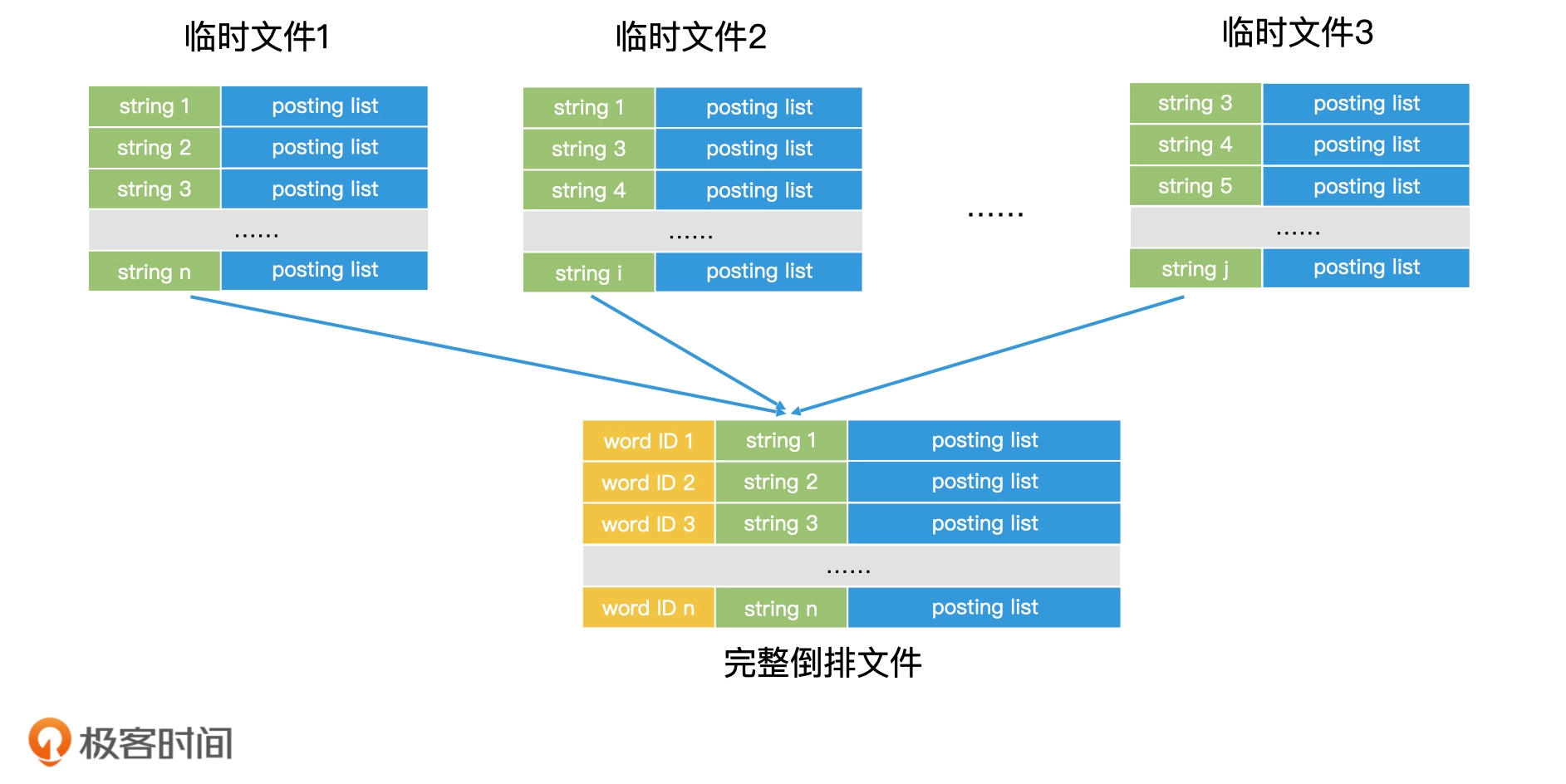
索引查询
对于能加载到内存中的文档列表,这没什么问题
但如果某些热词对应的文档列表过大,则需要利用磁盘索引数据结构,进行分层加载
索引更新
Double Buffer
为了避免读写竞争问题,可以在内存中同时保存两份一样的索引,一个是索引 A,一个是索引 B。我们会使用一个指针 p 指向索引 A,表示索引 A 是当前可访问的索引。那么用户在访问时就会通过指针 p 去访问索引 A。这个时候,如果我们要更新,只更新索引 B,当两份数据进行切换时,可以通过简单的原子操作修改引用即可
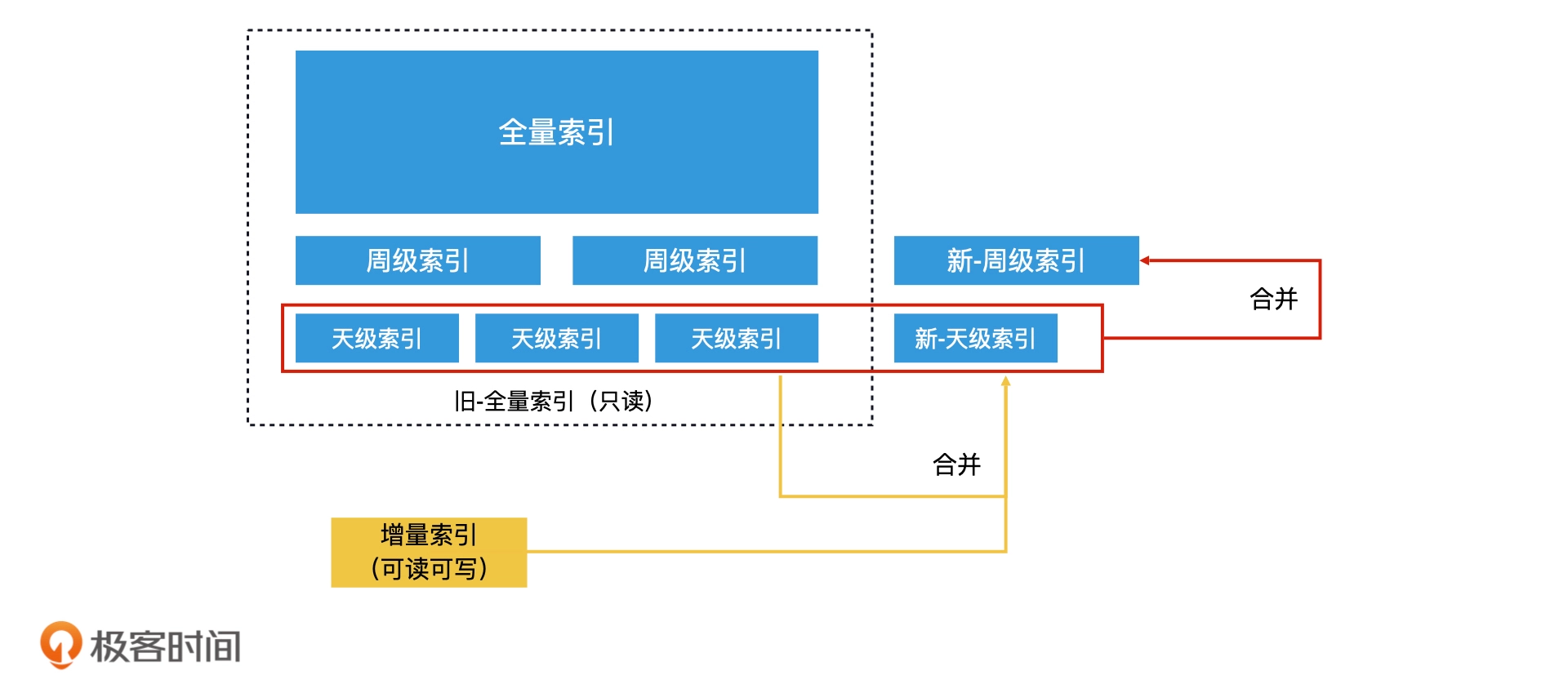
全量索引结合增量索引
系统会周期性地处理全部的数据,生成一份完整的索引,也就是全量索引。这个索引不可以被实时修改,对于要更新的索引,在内存构建一份增量索引,当查询发生的时候,会同时查询全量索引和增量索引,将合并的结果作为总的结果输出
将增量索引合并到全量索引中的常见方法有 3 种:
- 完全重建法:在增量索引写满内存空间之前,完全重建一次全量索引,然后将系统查询切换到新的全量索引上
- 再合并法:对增量索引与全量索引进行归并
- 滚动合并法:当内存中的增量索引增长到一定体量时,先合并到天级索引,天级索引量够了,再合并到月级索引,以此类推
索引拆分
基本原理跟分库分表是一样的
- 基于业务拆分:不同类型的文档分区存储,查询时根据业务需求到指定的索引分区上
- 水平拆分:通过哈希的方式,将文档分区,查询时并行查询多个索引,再进行合并
- 基于关键词拆分:水平拆分的细化,通过关键词作为分区依据
文档搜索排序
TF-IDF 算法
相关性 = TF*IDF
TF 是词频(Term Frequency),IDF 是逆文档频率(Inverse Document Frequency)
- 词频定义的就是一个词项在文档中出现的次数
- 文档频率(Document Frequency),指的是这个词项出现在了多少个文档中
- 逆文档频率是对文档频率取倒数,它的值越大,这个词的的区分度就越大
BM25 算法
BM25 算法认为词频和相关性的关系并不是线性的。也就是说,随着词频的增加,相关性的增加会越来越不明显,并且还会有一个阈值上限
PageRank
将所有的网页视作节点(node),而将超链接视作边(edge)。每个节点的权重值表示对应的页面的重要度。通向该网页的超链接称做“对该网页的投票(a vote of support)”。每个网页的权重值大小被递归地定义,依托于所有链接该页面的页面的权重值
逻辑回归模型
把不同的打分因子进行加权求和
Score = w1 * x1 + w2 * x2 + w3 * x3 + …… + wn * xn
非精准TOPK检索
- 尽可能地将计算放到离线环节,只需要保证质量足够高的结果,被包含在最终的 Top K 个结果中就够了
- 根据静态质量得分排序截断:需要将每个词对应的文档列表按分数排序,在查询时进行归并并返回前K个
- 根据词频得分排序截断:文档列表按词频排序
- 一个问题就是词频相同如何排序,一个解决办法就是胜者表:根据某种权重将文档列表中的元素进行排序,并提前截取 r 个最优结果,但这种方式有可能造成没法取得足够的K个文档,造成检索结果的丢失
- 分层索引:先离线给所有文档完成打分,然后将得分最高的 m 个文档作为高分文档,单独建立一个高质量索引,其他的文档则作为低质量索引
- 查询时,如果高质量索引中的检索结果不足 k 个,那我们再去低质量索引中查询,补全到 k 个结果
空间检索
空间信息存储
几何信息表示:包括点、线、多边形等几何要素的坐标表示,以及与之相关的属性信息
地理数据表示:
- 矢量数据:由顶点和路径组成,矢量多边形是一组封闭的顶点和路径
- 光栅数据:栅格由像素或网格单元组成,栅格通常看起来像素化,因为每个像素都有自己的值或类别
模糊查询TOPK
先将经纬度转换为一个固定的区域,查询时只对这个区域内的数据进行距离计算
这种非精准检索的方案,会带来一定的误差,找到的只是这个区域内距离最近的,而非实际距离最近的
精确查询TOPK
区域粒度过粗,就会有上面的那个问题,如果是较细粒度的区域划分,则可以对当前区域周边的8个方位都发起查询,这样就精确了
Geohash 编码
- 将经纬度坐标转换为字符串的编码方式
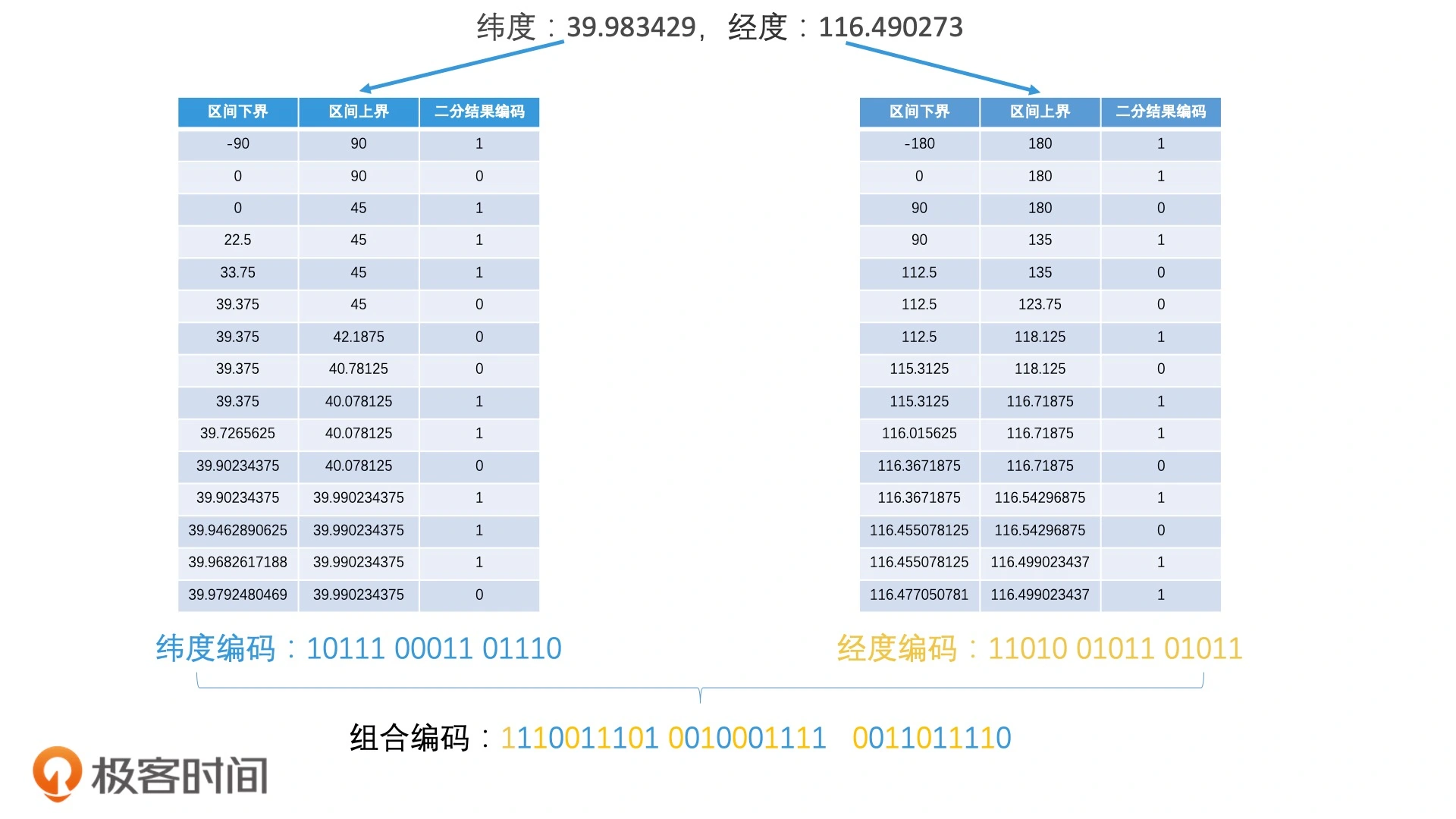
使用 GeoHash 编码后,相当于把整个地理空间划分成了一个个方格,每个方格对应了 GeoHash 中的一个分区
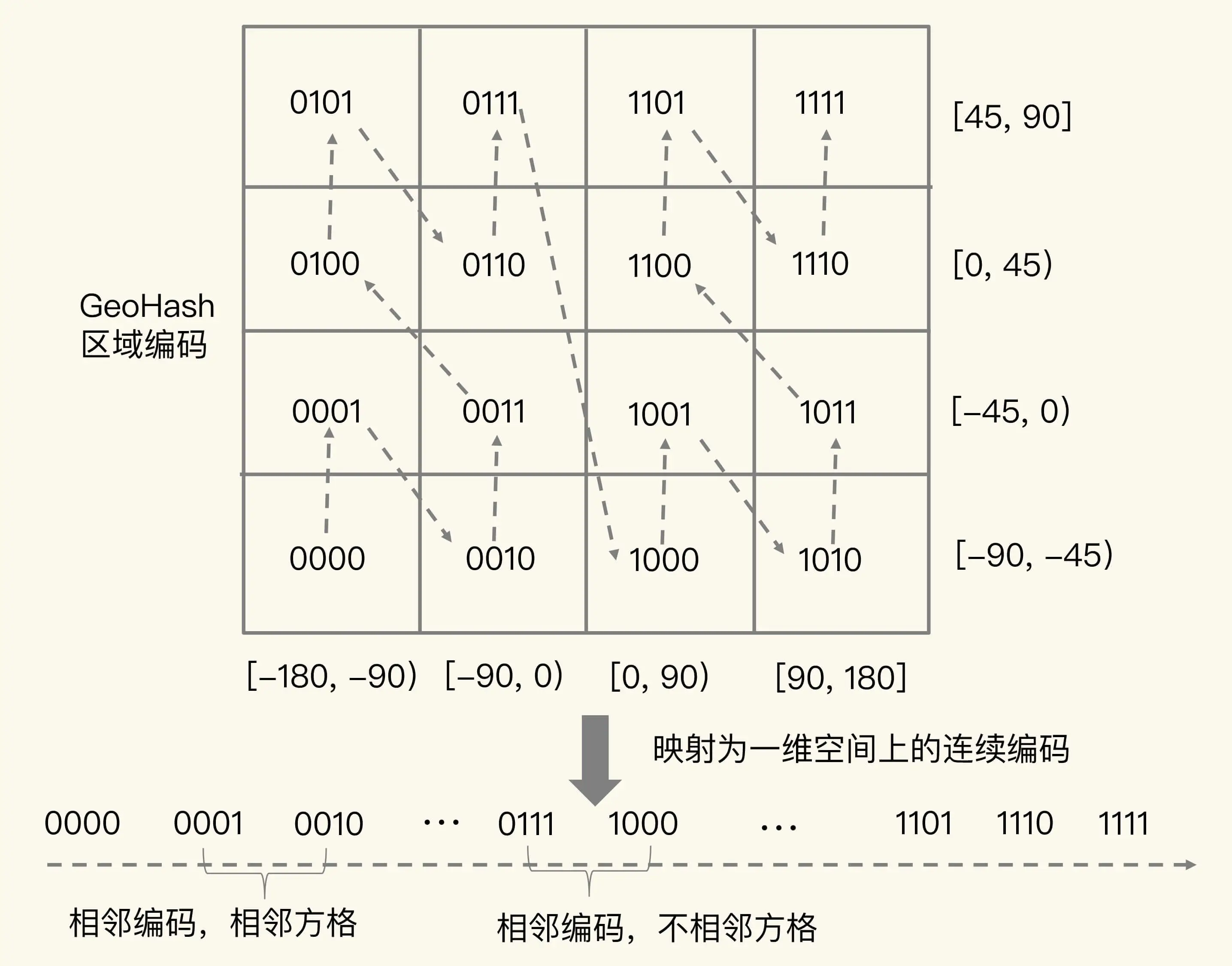
字符长度和覆盖区域对照表:
| Geohash编码长度 | 宽度 | 高度 |
|---|---|---|
| 1 | 5009.4km | 4992.6km |
| 2 | 1252.3km | 624.1km |
| 3 | 156.5km | 156km |
| 4 | 39.1km | 19.5km |
| 5 | 4.9km | 4.9km |
| 6 | 1.2km | 609.4m |
| 7 | 152.9m | 152.4m |
| 8 | 38.2m | 19m |
| 9 | 4.8m | 4.8m |
| 10 | 1.2m | 59.5cm |
| 11 | 14.9cm | 14.9cm |
| 12 | 3.7cm | 1.9cm |
最近精确查询
先获得当前位置的 GeoHash 编码,然后根据需求不停扩大查询范围进行多次查询,最后合并查询结果
在检索完 wx4g6yc8 这个区域编码以后,如果结果数量不够,还要检索 wx4g6yc 这个更大范围的区域编码,我们只要将查询改写为“查找区域编码在 wx4g6yc0 至 wx4g6ycz 之间的元素”,就可以利用同一个索引,来完成更高一个层级的区域查询了
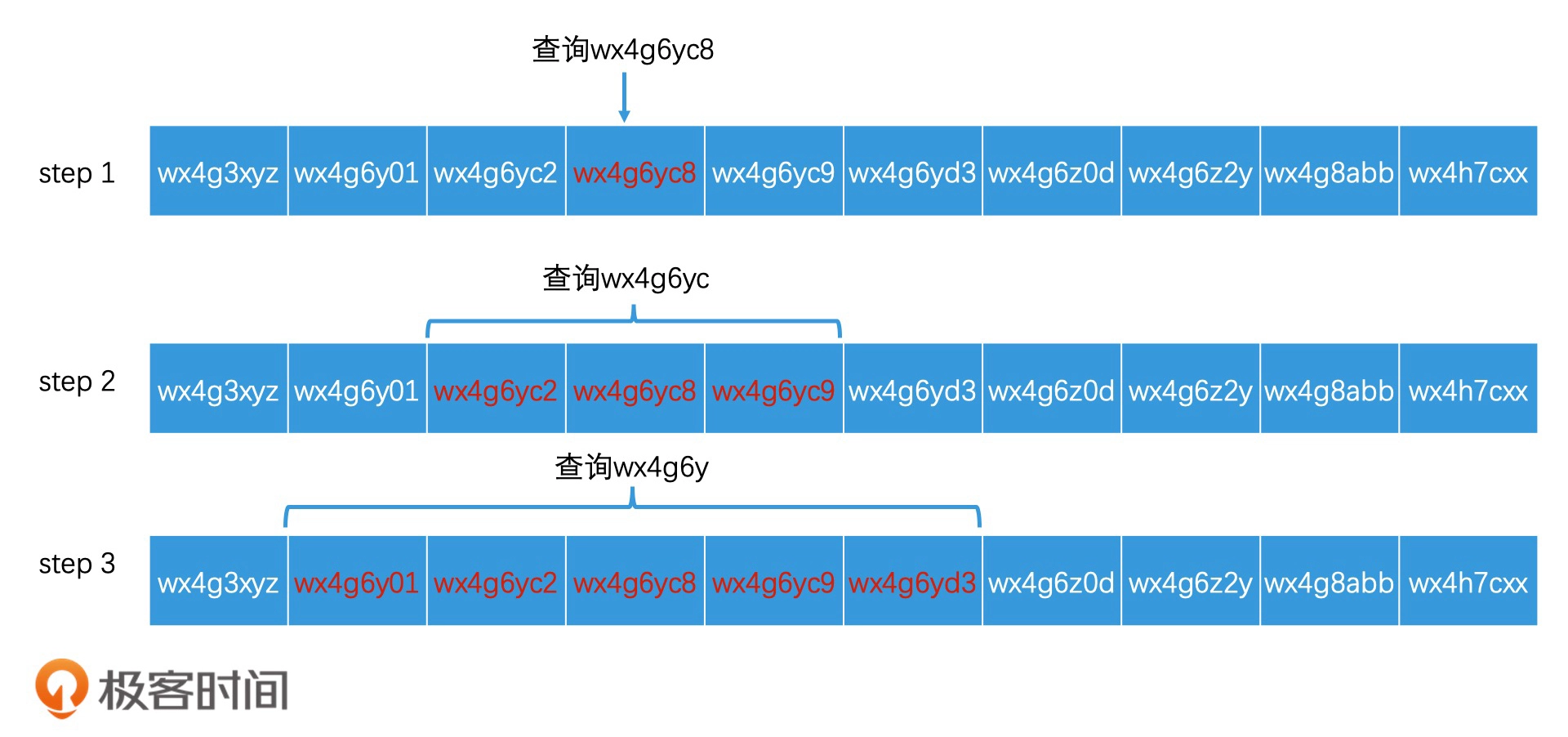
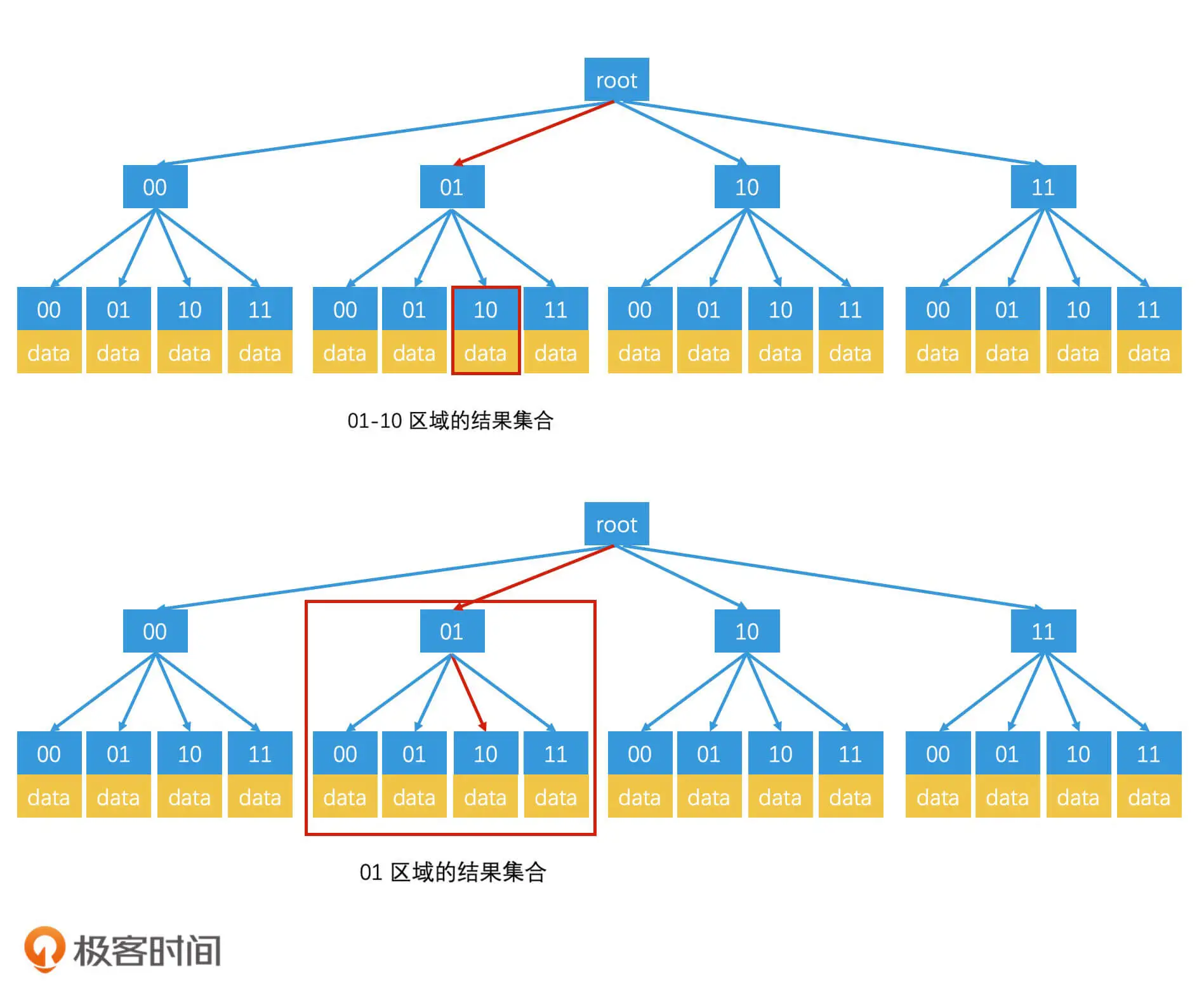
这个时候需要引入四叉树,就可以逐层地往外找
另外一种查询方式是前缀树:
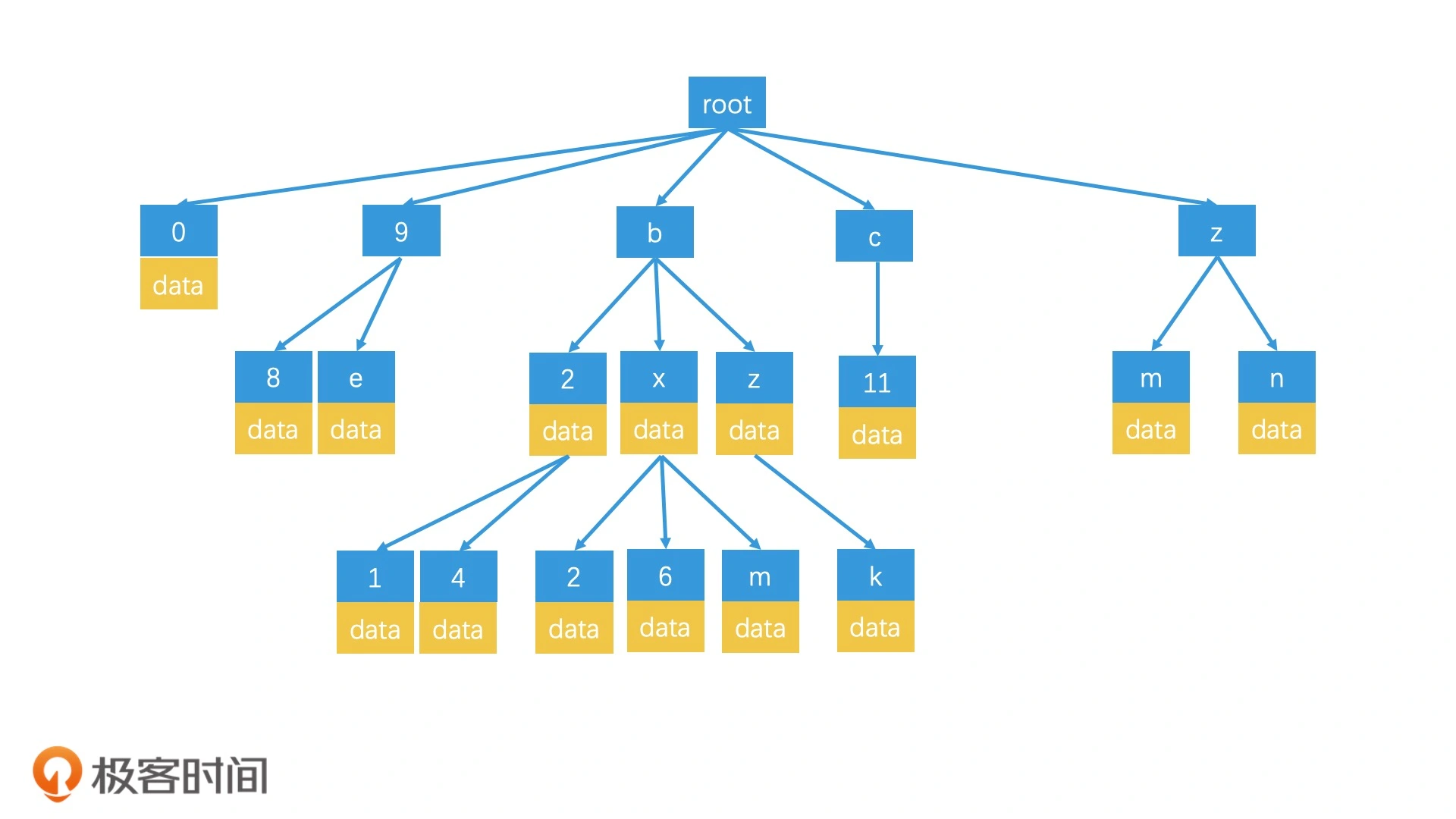
当我们查询 wx4g6yc8 这个区域时,我们会沿着 w-x-4-g-6-y-c-8 的路径,检索到对应的叶子节点,然后取出这个叶子节点上存储的数据。如果这个区域的数据不足 k 个,就返回到父节点上,检索对应的区域,直到返回结果达到 k 个为止
近似最近邻检索
局部敏感哈希
- 相似的数据通过哈希计算后,生成的哈希值是相近的(甚至是相等的),局部敏感哈希的基本思想是希望让相邻的点落入同一个“桶”,这样在进行最近邻搜索时,我们仅需要在一个桶内,或相邻几个桶内的元素中进行搜索即可
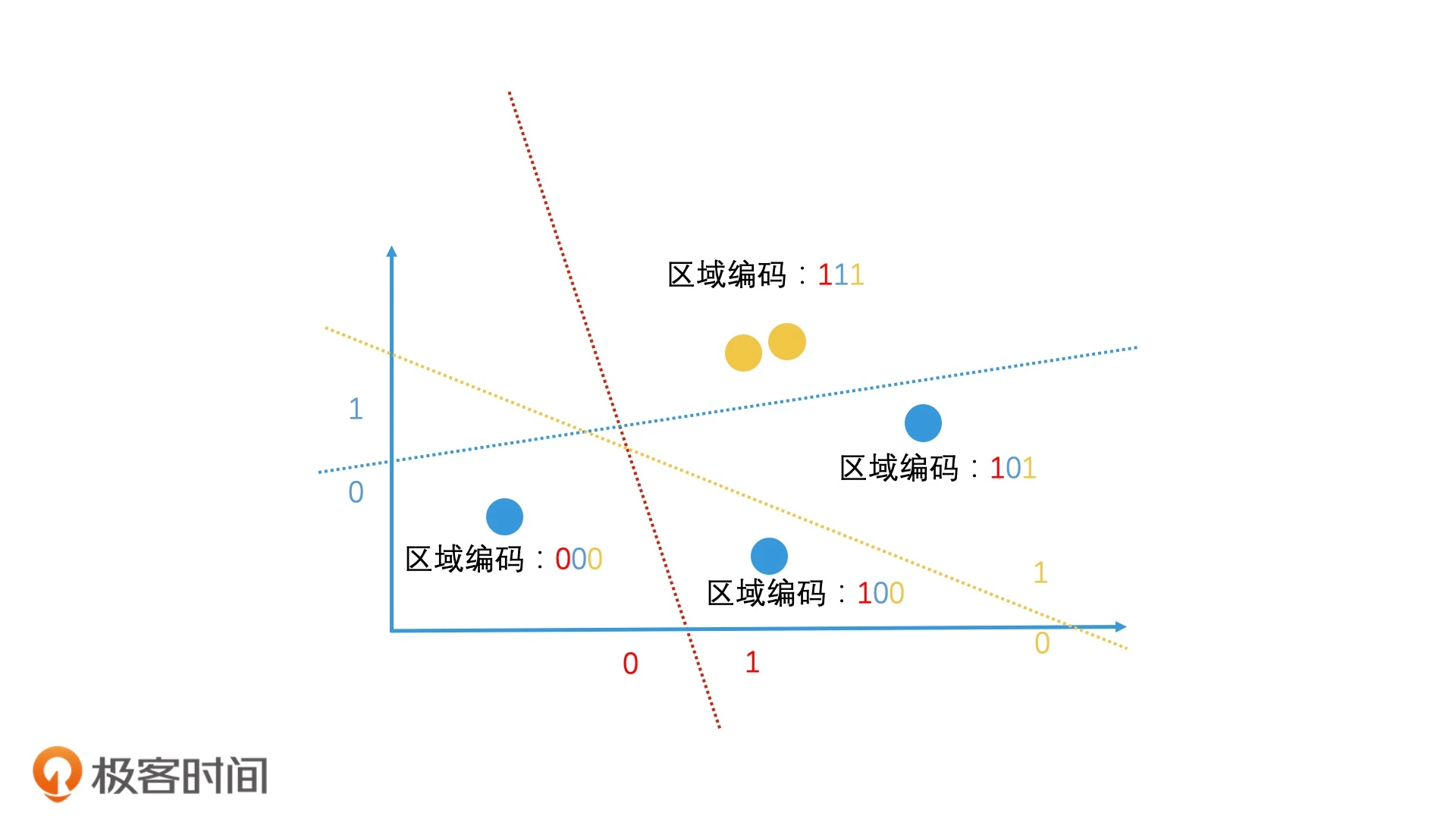
如果连续做了 n 次这样的随机划分,这两个点每次都在同一边,那就可以认为它们在很大概率上是相近的
实际上,在利用局部敏感哈希值来判断文章相似性的时候,会以表示比特位差异数的海明距离(Hamming Distance)为标准,即比特位数的差异数
SimHash
- 选择一个能将关键词映射到 64 位正整数的普通哈希函数
- 使用该哈希函数给文档中的每个关键词生成一个 64 位的哈希值,并将该哈希值中的 0 修改为 -1。比如说,关键词 A 的哈希值编码为 <1,0,1,1,0>,那我们做完转换以后,编码就变成了 <1,-1,1,1,-1>
- 将关键词的编码乘上关键词自己的权重。如果关键词编码为 <1,-1,1,1,-1>,关键词的权重为 2,最后我们得到的关键词编码就变成了 <2,-2,2,2,-2>
- 将所有关键词的编码按位相加,合成一个编码如果两个关键词的编码分别为 <2,-2,2,2,-2> 和 `<3,3,-3,3,3>`,那它们相加以后就会得到 <5,1,-1,5,1>
- 将最终得到的编码中大于 0 的值变为 1,小于等于 0 的变为 0。这样,编码 <5,1,-1,5, 1> 就会被转换为 <1,1,0,1,1>
相似检索
将所有的文档根据自己每个比特位的值,加入到对应的倒排索引的 posting list 中,当需要查询与该文档相似的其他文档时:
- 计算出待查询文档的 SimHash 值
- 以该 SimHash 值中每个比特位的值作为 Key,去倒排索引中查询,将相同位置具有相同值的文档都召回
- 合并这些文档,并一一判断它们和要查询的文档之间的海明距离是否在 3 之内,留下满足条件的
只要有一个比特位的值相同,文档就会被召回。也就是说,这个方案和遍历所有文档相比,其实只能排除掉“比特位完全不同的文档”,一种优化是Google 的抽屉原理:
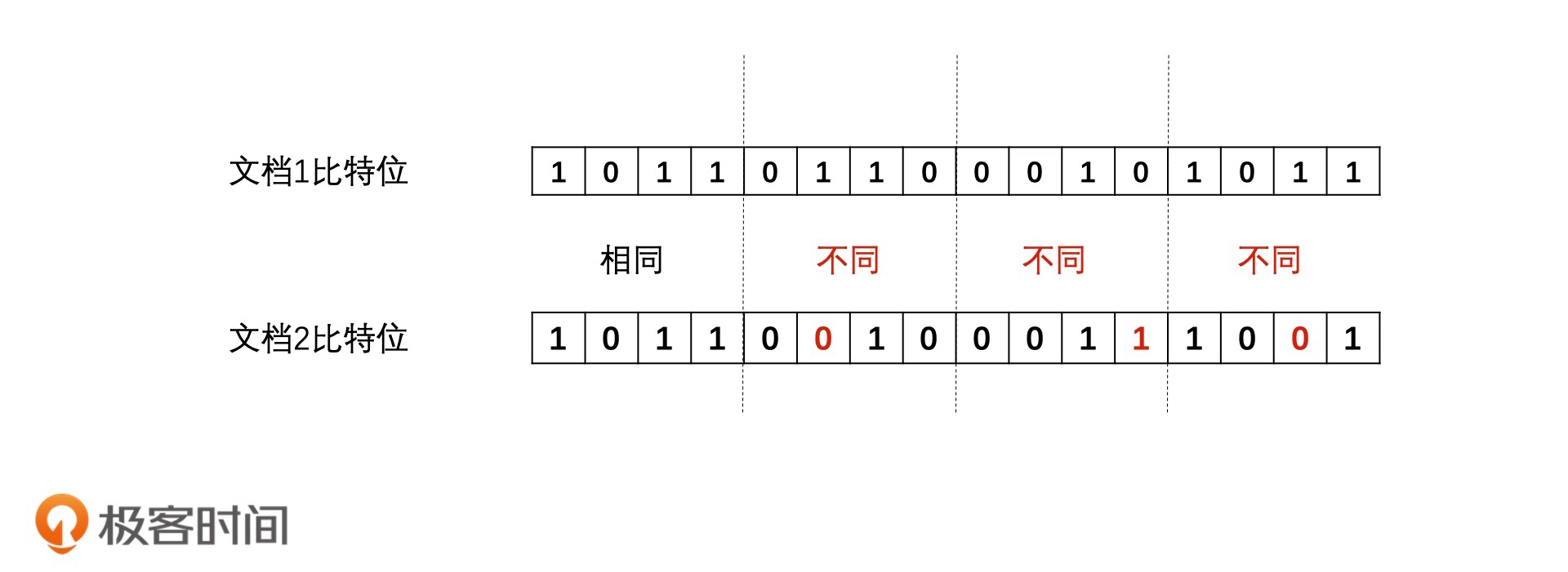
将每一个文档都根据比特位划分为 4 段,以每一段的 16 个比特位的值作为 Key,建立 4 个倒排索引。检索的时候,我们会把要查询文档的 SimHash 值也分为 4 段,然后分别去对应的倒排索引中,查询和自己这一段比特位完全相同的文档。最后,将返回的四个 posting list 合并,并一一判断它们的的海明距离是否在 3 之内
乘积量化
量化指的就是将一个空间划分为多个区域,然后为每个区域编码标识,乘积指的是高维空间可以看作是由多个低维空间相乘得到的
乘积量化其实就是将向量的高维空间看成是多个子空间的乘积,然后针对每个子空间,再用聚类技术分成多个区域。最后,给每个区域生成一个唯一编码,也就是聚类 ID
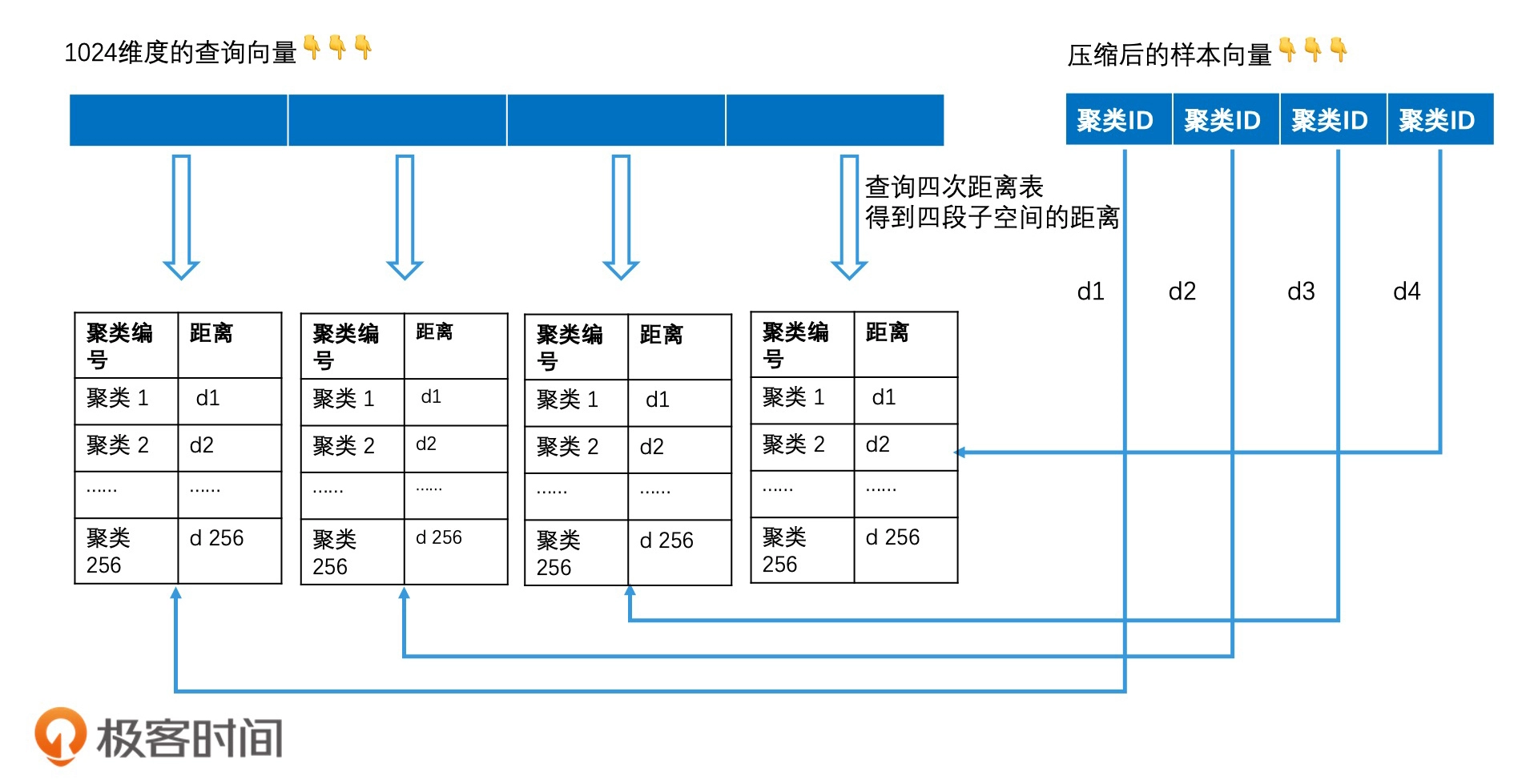
对乘积量化进行倒排索引:
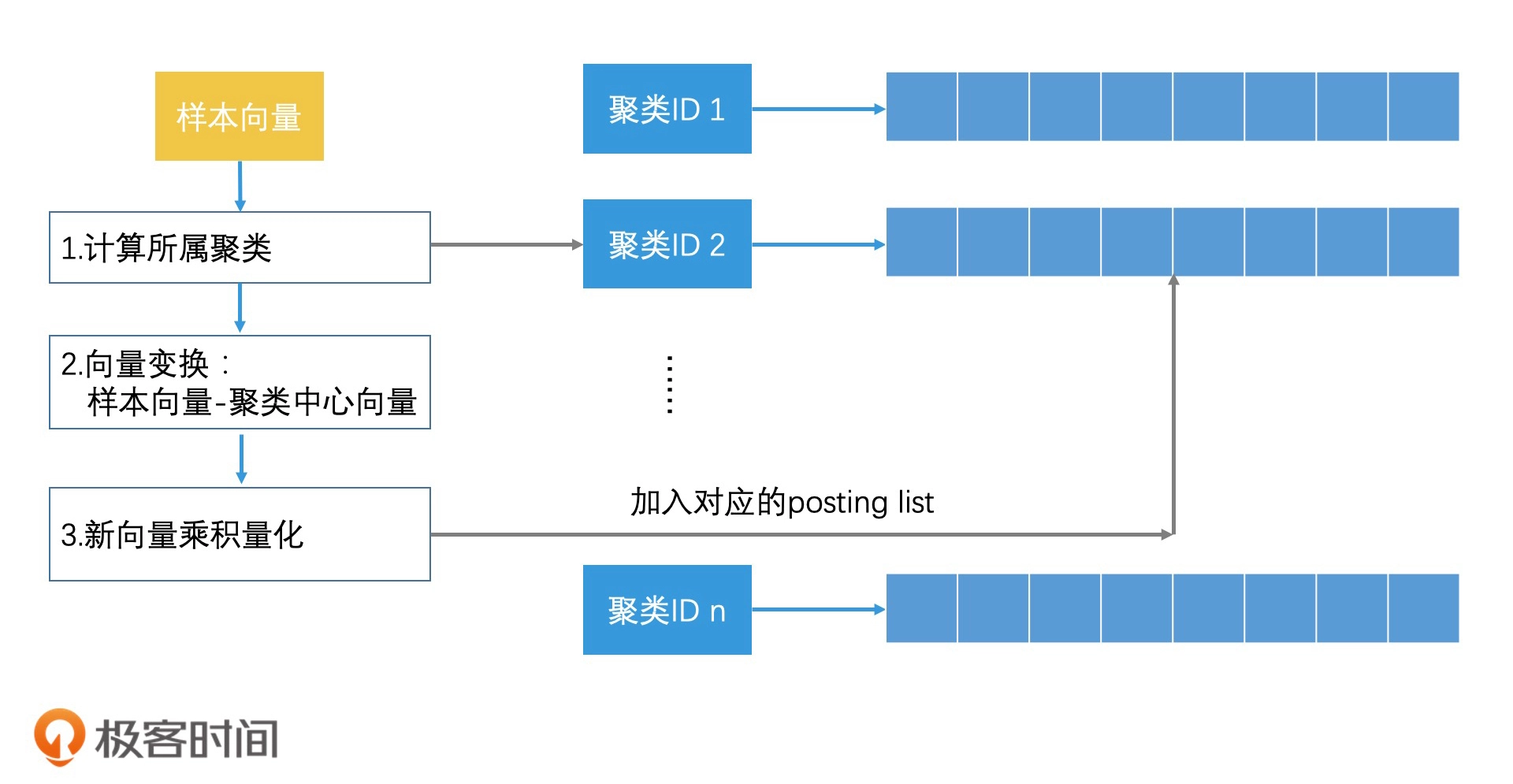

HNSW
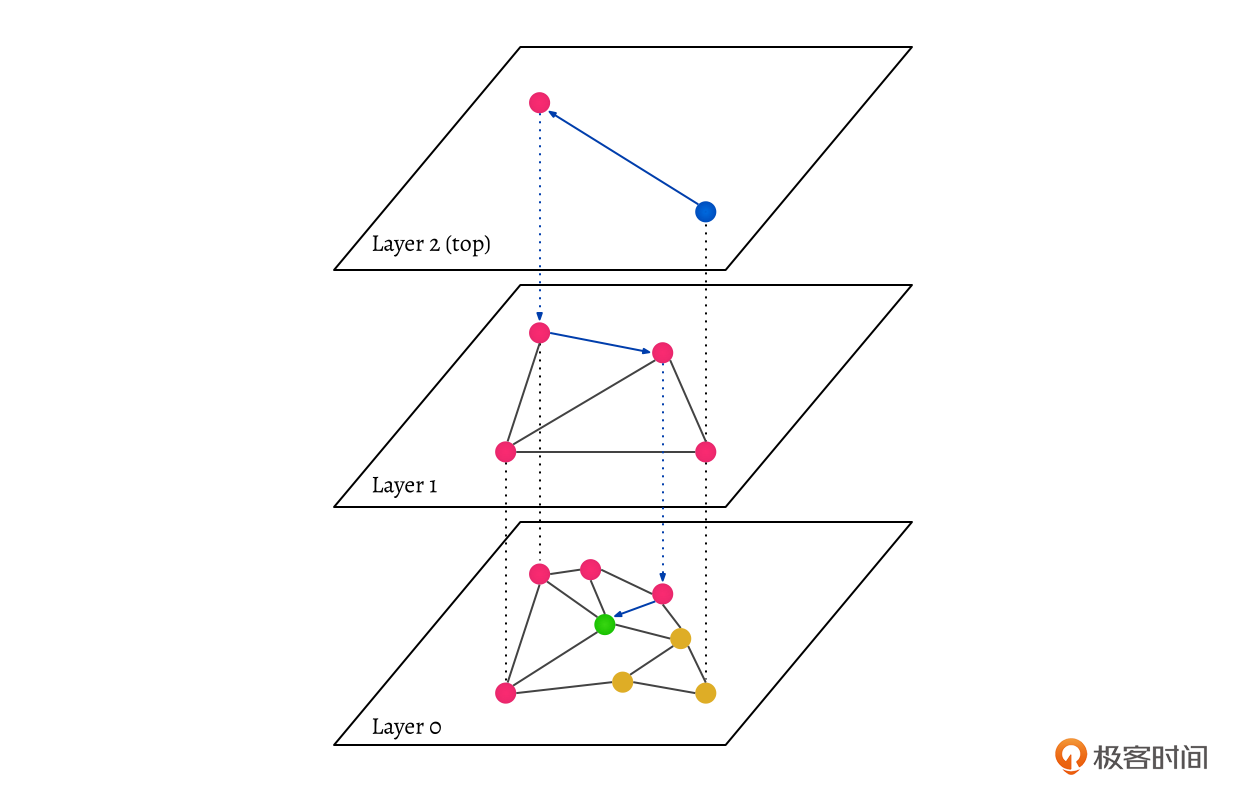
- (Hierarchical Navigable Small World,分层导航小世界图)
搜索的时候会从顶层开始,在每层里,算法会选择与当前点最近的节点,然后移动到这个节点。当无法进一步接近时,搜索就下降一层,直到达到最底层。这个过程类似于跳表的查找过程
RAG
RAG 将传统的语言生成模型与大规模的外部知识库相结合,使模型在生成响应或文本时可以动态地从这些知识库中检索相关信息
- 检索:对于给定的输入(问题),模型首先使用检索系统从大型文档集合中查找相关的文档或段落。这个检索系统通常基于密集向量搜索,例如 ChromaDB、Faiss 这样的向量数据库
- 上下文编码:找到相关的文档或段落后,模型将它们与原始输入(问题)一起编码
- 生成:使用编码的上下文信息,模型生成输出(答案)。这通常当然是通过大模型完成的
基于 Faiss 实现实时人像追踪
sequenceDiagram 前端摄像头 ->> 网关: 人脸数据 网关 ->> Kafka: (人脸数据,位置,时间,身份) Kafka ->> FaceConsumer: FaceConsumer -->> FaceConsumer: 将人脸转为向量 FaceConsumer ->> Storage: 存储向量,<br>生成唯一ID FaceConsumer ->> Storage: 存储唯一ID与位置、时间、身份 FaceService ->> Storage: 获取向量 FaceService -->> FaceService: Faiss 构建索引 使用者 -->> FaceService: 提供一个人脸向量 FaceService ->> FaceService: 返回最相关的k个向量ID FaceService ->> FaceService: 根据K个向量ID构建行踪轨迹索引类型与空间占用
使用 Faiss 的 IndexFlatL2,这个方法是精确搜索。128 维的人脸向量,一千万的索引,约占 5G 内存空间。
数据量
某二线城市,一个区县约有 3 万台人像识别设备,一天越能产生一千万的人像数据,整座城市一天算下来越可以产生 7 千万到 1.2 亿的人像数据。
大约 50 个进程就能支撑起一座城市 7 天的实时人像数据检索需求。
三台 128G 内存的机器,就能支撑起上面这个需求。
性能与问题
效果:k = 500 时,单进程一秒内返回结果
遇到的一些问题:
- 大量人脸小文件造成 inode 耗尽,导致无法写入文件。只能扩容磁盘或重写格式化,增加 inode 数量
- 对于历史数据,单进程人脸转向量时,速度较慢,启用多进程
水平扩展
stateDiagram-v2 master --> process1(1,10000000) master --> process2(10000001,20000000) master --> process3(20000001,30000000) master --> ...通过不同的进程各负责一部分的向量处理以及识别,再由 master 聚合结果。实现水平扩展